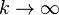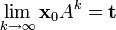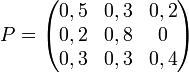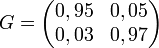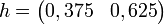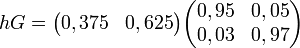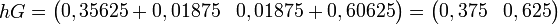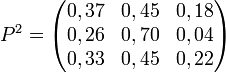Matrice stochastique - Définition
En mathématiques, une matrice stochastique (aussi appelée matrice de Markov) est une matrice carrée dont chaque élément est un réel compris entre 0 et 1 et dont la somme des éléments de chaque ligne vaut 1. Cela correspond, en probabilité, à la matrice de transition d'une chaîne de Markov finie.
Voici un exemple de matrice stochastique P (dans cet exemple, la somme des éléments de chaque ligne est égale à 1; on remarque que la somme des éléments de chaque colonne est quelconque):
Si G est une matrice stochastique, alors on appelle vecteur stable pour G le vecteur h tel que:
- hG = h
Par exemple:
et
Cet exemple montre que hG = 1h. Pour des équations du type hG = βh, où β est un nombre réel , on dit que h est un vecteur propre associé à la valeur propre β. On peut donc dire que h est un vecteur propre associé à la valeur propre 1.
Une matrice stochastique est dite régulière s'il existe un entier k tel que la matrice Pk ne contient que des réels strictement positifs.
La matrice 3 × 3 précédente est régulière car :
Le théorème des matrices stochastiques stipule que, si A est une matrice stochastique régulière, alors A possède un vecteur stable t tel que, si xo est un état initial quelconque, et si xk+1 = xkA pour k = 0, 1, 2, ..... alors la chaîne de Markov {xk} converge vers t quand