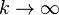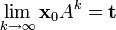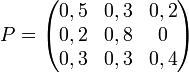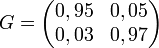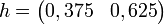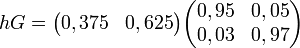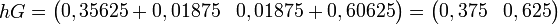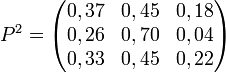Matrice stochastique - Définition
La liste des auteurs de cet article est disponible ici.
En mathématiques, une matrice stochastique (aussi appelée matrice de Markov) est une matrice carrée dont chaque élément est un réel compris entre 0 et 1 et dont la somme des éléments de chaque ligne vaut 1. Cela correspond, en probabilité, à la matrice de transition d'une chaîne de Markov finie.
Une matrice est dite doublement stochastique si la somme des éléments de chaque ligne et de chaque colonne vaut 1.
Voici un exemple de matrice stochastique P (dans cet exemple, la somme des éléments de chaque ligne est égale à 1 ; on remarque que la somme des éléments de chaque colonne est quelconque):
Si G est une matrice stochastique, alors on appelle vecteur stable pour G un vecteur h tel que :
- hG = h
Par exemple :
et
Cet exemple montre que hG = 1h.
Pour des équations du type hG = βh, où β est un nombre réel, on dit que h est un vecteur propre associé à la valeur propre β. On peut donc dire que h est un vecteur propre associé à la valeur propre 1.
Une matrice stochastique est dite régulière s'il existe un entier k tel que la matrice Pk ne contient que des réels strictement positifs.
La matrice 3 × 3 précédente est régulière car :
Le théorème des matrices stochastiques stipule que, si A est une matrice stochastique régulière, alors
- la chaîne de Markov de matrice de transition A est irréductible ;
- l'espace vectoriel des vecteurs stables est de dimension 1 (les vecteurs stables sont tous colinéaires),
- A possède un unique vecteur stable t dont la somme des coordonnées vaut 1,
- les coordonnées de t sont toutes strictement positives.
De plus, si xo est une loi initiale quelconque (i.e. est un vecteur à coordonnées positives ou nulles et de somme 1), et si xk+1 = xkA pour k = 0, 1, 2, ..... alors la chaîne de Markov {xk} converge vers t quand