Fonction numérique - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Lorsque nous exprimons qu’une quantité dépend d’une autre quantité nous supposons qu’il existe un moyen d’obtenir cette quantité à partir d’une autre. Et si ces quantités sont représentées par des variables, alors une variable est fonction d’une autre, quand il y a une règle qui permet d’obtenir la valeur de cette variable, à partir de la valeur de l’autre.
Exemple: la quantité "chiffre d'affaire" d'une entreprise dépend de la quantité "nb de produits vendus"
Une fonction numérique est une règle qui permet d'associer à un réel un autre nombre réel.
Donnons l’exemple d’un épicier qui augmente les prix de tous ses articles de 20%. Ajouter à chaque prix 20% du prix, revient à multiplier chaque prix par 120%. La règle que l’épicier va appliquer à chaque prix est la multiplication par 1,2 et nous dirons que le nouveau prix est fonction de l’ancien.
Définition
Une fonction numérique f ou fonction réelle d’une variable réelle d’une partie D de


Ce réel f(x) est l’image de x par f.
Cette partie D de

Notation
Nous notons la fonction :
(observer que la seconde flèche possède un poussoir que n'a pas la première)
- ou plus simplement
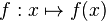
Exemple
Soit la fonction qui à tout nombre réel de l'intervalle [ − 1; + 1] associe son carré diminué de 1.
Nous pouvons définir la fonction f des manières suivantes :
Soit f définie par :
- pour tout réel x dans
![[ -1 ; +1 ],\ f(x) = x^2 - 1](https://static.techno-science.net/illustration/Definitions/autres/e/e038d2a4a9076024c4decda27d67d9d0_0969597aecffb441a1ce1cbdd11b828b.png)
ou encore :
Remarque
Nous ne devons pas confondre f et f(x). Dans l’exemple précédent f est la règle qui élève un réel au carré et lui retranche 1, tandis que f(x) est égal au réel x²-1 qui est associé à x.
Ensemble de définition
Soit f une fonction de D dans

Soit x un réel. Si x appartient à D, alors on dit que f est définie en x, et si x n’appartient pas à D on dit que f n’est pas définie en x.
Remarques
- L'ensemble de définition d'une fonction peut être donné dans l'énoncé définissant la fonction et sinon il doit être déterminé.
- Rechercher l’ensemble de définition ou le domaine de définition d’une fonction, c’est déterminer les réels x tels que f(x) existe.
Erreurs classiques
Bon nombre de lycéens tiennent pour vraie la relation f(a+b)=f(a)+f(b) :
- pour la fonction carré, cela donnerait (a+b)²=a²+b², ce qui est faux (voir identité remarquable) ;
- pour la fonction sinus, cela donnerait sin(a+b)=sin(a)+sin(b) donc 0=sin(180°)=sin(90°+90°)=sin(90°)+sin(90°)=2, soit 0=2 (voir fonction trigonométrique ;
- pour la fonction logarithme, cela donnerait ln(a+b)=ln(a)+ln(b) donc ln(2)=ln(1)+ln(1)=0, ce qui est encore faux.
En fait la confusion vient de l’application abusive des règles de calcul uniquement valables pour les fonctions linéaires, en d’autres mots pour les situations de proportionnalité.
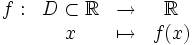
![\begin{matrix}f: & [-1;1] & \rightarrow & \mathbb R\\ & x & \mapsto & f(x) = x^2-1\end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/2/2ec32b6dccbfd466c6ea341ebdf5de66_fe47f7bde52fa7dd1128013c870cf0d7.png)

















































