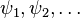Approximation orbitale - Définition

Un système chimique (molécules, ions...) est constitué de noyaux et d'électrons. Dans le cadre de l'approximation de Born-Oppenheimer, les électrons sont décrits collectivement par une fonction d'onde dite multiélectronique . Cette fonction d'onde décrit la probabilité de trouver simultanément l'électron 1 à la position r₁ et l'électron 2 à la position r₂, etc. Ceci a pour conséquence que la probabilité de trouver l'électron 1 à un endroit donné dépend de la position de l'électron 2 : on dit que les électrons sont corrélés.

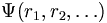
La fonction d'onde satisfait l'équation de Schrödinger :

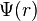
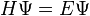
H est un opérateur appelé hamiltonien, est la fonction d'onde et E est l'état énergétique associé à cette fonction d'onde. La fonction d'onde peut être décrite soit avec les coordonnées cartésiennes x,y et z, soit avec les coordonnées sphériques r, et  :

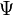
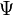
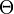
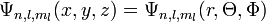
Les indices n, l et ml sont les trois nombres quantiques décrivant les orbitales atomiques de l'électron :

• n est le nombre quantique principal.
• l est le nombre quantique secondaire (ou azimuthal).
• ml est le nombre quantique tertiaire (ou magnétique).

L'approximation orbitale consiste à supposer que les électrons sont pratiquements indépendants les uns des autres, ce qui permet de simplifier l'écriture de la fonction d'onde :

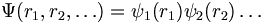
Mais cette approximation n'est pas satisfaisante car il existe des interactions entre le noyau chargé positivement et les électrons ainsi qu'entre les électrons eux-mêmes. Pour s'approcher des valeurs établies expérimentalement on utilise les règles de Slater qui permettent de moyenner pour chaque électron la charge effective : c'est le deuxième niveau d'approximation.

Chacune des fonctions d'onde décrit un seul électron : ce sont des fonctions d'onde monoélectroniques. Les fonctions d'ondes monoélectroniques décrivant les états stationnaires des électrons sont appelées orbitales. Dans un atome, on parle d'orbitale atomique, et, lorsque les orbitales atomiques de plusieurs atomes interagissent, d'orbitale moléculaire.