Addition - Définition
La liste des auteurs de cet article est disponible ici.
Opération numérique
Notation

L'addition de deux termes a et b se note habituellement a + b et se lit « a plus b », parfois « a et b » ou « a ajouté à b ».
Le signe « + » remplace depuis la fin du XVe siècle le symbole p pour « plus ».
Cette notation infixe peut être remplacée dans certains contextes par une notation fonctionnelle + (a,b) ou par une notation postfixée (a)(b) + .
Dans la décomposition arborescente d'une expression algébrique, l'addition est représentée par un nœud trivalent avec deux entrées et une sortie.
|
| |
| |
|
|
|
|
Dans un système de notation additive tel que le système unaire ou la numération égyptienne, le signe « + » n'a pas besoin d'être indiqué puisque l'écriture des nombres consiste déjà à décomposer les nombres en une somme de valeurs numériques fixées.
Dans un système de notation positionnelle telle la notation moderne, l'addition de plusieurs nombres est parfois représentée par la superposition des écritures de nombres, tous les chiffres d'une même position étant alignés verticalement. Cette disposition facilite le de la somme de plusieurs nombres.
Propriétés
L'addition de nombres possède certaines propriétés valables dans tous les ensembles de nombres usuels :
- elle est commutative, c'est-à-dire que l'ordre dans lequel sont donnés les termes de l'addition n'a pas d'influence sur le résultat :
a + b = b + a ;
- elle est associative, c'est-à-dire qu'il n'y a pas besoin de préciser par des parenthèses l'ordre dans lequel est effectuée une suite d'additions :
(a + b) + c = a + (b + c), d'où la notation sans parenthèses a + b + c ;
- elle est simplifiable, c'est-à-dire que dans une égalité d'additions, on peut supprimer deux termes identiques de part et d'autre du signe égal :
si x + a = y + a alors x = y ;
- l'élément nul ou zéro, noté 0, est neutre pour l'addition :
a + 0 = a.
Chaque nombre x possède un symétrique pour l'addition, appelé « opposé » et noté − x, c'est-à-dire tel que x + ( − x) = − x + x = 0.
Les ensembles de nombres



L'addition avec un symétrique permet de définir la soustraction par x − y = x + ( − y).
Procédé de calcul
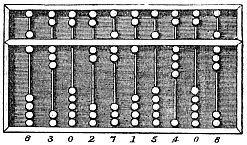
L'évaluation du résultat d'une addition dépend du système de numération employé, c'est-à-dire de la manière de représenter les nombres.
Dans un système additif, il suffit de juxtaposer les écritures puis de simplifier l'expression en regroupant les symboles de même valeur pour en remplacer une partie par des symboles de valeur plus élevée lorsque c'est possible. De manière générale, les systèmes de numération non chiffrés ont pu développer une technique d'addition par la pratique de l'abaque.
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Table d'addition en écriture positionnelle décimale | ||||||||||
Dans un système de numération positionnelle chiffrée, le calcul d'une somme d'entiers passe par l'utilisation d'une table d'addition. Celle-ci permet de trouver la somme des chiffres sur chaque position.
L'écriture du résultat se fait de la position la plus basse à la position la plus haute (de droite à gauche en notation moderne). Pour chaque position, on inscrit le chiffre des unités de la somme des chiffres et on reporte une retenue sur la position suivante si cette somme est plus grande que la base. Chaque chiffre du résultat est ensuite incrémenté de l'éventuelle retenue.
Pour clarifier visuellement le procédé, on peut commencer par poser l'addition, c'est-à-dire, en notation moderne, écrire l'un en dessous de l'autre les nombres à additionner en alignant verticalement les positions correspondantes.
Cette méthode se généralise pour les nombres décimaux en alignant verticalement les virgules.
L'addition de fractions d'entiers passe par une mise au même dénominateur, puis une addition des numérateurs et enfin par une éventuelle simplification de la fraction obtenue.
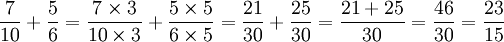
Quant à l'addition des fractions égyptiennes de numérateur unitaire et de dénominateurs tous distincts, elle fait appel à un processus itératif de simplification des fractions apparaissant en double.
Les sommes d'entiers, de décimaux et de rationnels peuvent toujours se ramener à une forme où ne figure plus le signe « + ». En revanche, une somme de réels n'admet pas toujours une telle forme : on ne peut pas simplifier l'écriture de 1 + √2.
Itération
En choisissant un terme constant r, l'addition permet de définir une fonction
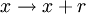
De telles suites (un) vérifient pour tout entier positif n la relation un + 1 = un + r. Elles s'écrivent alors sous la forme :
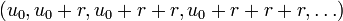
Ces répétitions d'addition permettent de définir la multiplication par un nombre entier :
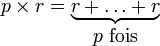
L'addition d'une suite finie de nombres définie par une formule générale (par exemple, l'addition des entiers impairs de 1 à 99) utilise des procédés spécifiques qui quittent le domaine opératoire de l'addition. L'étude des suites et séries associées fournit des méthodes plus efficaces pour le calcul de telles sommes.
Culture populaire
L'addition donne aussi lieu à certains jeux. La mourre, par exemple, consiste à deviner la somme de deux petits nombres, que les deux adversaires donnent simultanément avec leurs doigts.
En poésie, elle est évoquée par la Page d'écriture de Jacques Prévert.