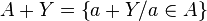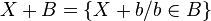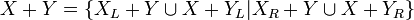Addition - Définition

Extensions

D'autres structures mathématiques étendent certains ensembles de nombres et sont munis d'une opération binaire qui prolonge l'addition usuelle, mais qui ne possède pas toujours toutes ses propriétés.

Fonctions

Si les applications définies sur un ensemble donné commun et à valeur numérique peuvent s'additionner simplement composante par composante comme des vecteurs, il n'en est pas de même pour les fonctions qui ont un domaine de définition propre.

Étant donné deux fonctions f et g définies sur les domaines respectifs D_f et D_g (par exemple des intervalles réels), la fonction f + g a pour domaine l'intersection et pour expression l'addition usuelle (f + g)(x) = f(x) + g(x).

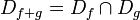
Cette addition est associative et commutative. Son neutre est la fonction définie partout et constamment nulle, mais l'addition d'une « fonction opposée » ne permet pas d'étendre le domaine de définition. Par exemple, la somme des fonctions et est la fonction nulle définie seulement sur les réels positifs.

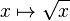
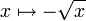
Dans certains contextes, comme dans l'addition des fonctions méromorphes, l'effacement des singularités permet cependant d'évacuer le problème du domaine de définition de la somme.

Variables aléatoires indépendantes

En probabilités élémentaires, étant données deux variables aléatoires indépendantes ne pouvant prendre qu'un nombre fini de valeurs, l'addition se calcule en construisant un tableau avec une ligne par valeur de la première variable et une colonne par valeur de la seconde variable.

Chaque case du tableau est remplie avec d'une part la somme des valeurs de la ligne et de la colonne correspondante, d'autre part le produit des probabilités correspondantes. Ensuite, il suffit pour chaque valeur apparaissant dans le tableau de faire la somme des probabilités des cases qui la contiennent.

En probabilités continues, la densité de probabilité d'une somme de deux variables aléatoires indépendantes est donnée par le produit de convolution des densités de probabilités initiales.
.

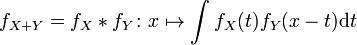
Cette présentation s'étend aux variables aléatoires dont la fonction de densité est une distribution.

Cette opération est associative et commutative. Le neutre est la variable aléatoire toujours nulle, mais seuls les nombres, représentés par les variables aléatoires constantes admettent des opposés. Il n'existe pas d'opposé aux variables aléatoires non constantes : elles sont d'étendue strictement positive, or l'étendue d'une somme est la somme des étendues.

Limites réelles

Les limites de suites ou de fonctions à valeur réelle peuvent être prises dans la droite continuée . L'addition des nombres peut alors s'étendre partiellement aux termes infinis. Pour tout x réel :

, et

.

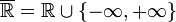
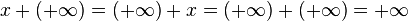
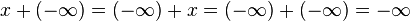
Cette opération garde des propriétés de commutativité et d'associativité mais n'est pas définie pour les couples et .

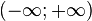
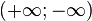
Selon les cas, la somme de deux suites ou fonctions admettant des limites infinies opposées peut avoir une limite finie, infinie ou pas de limite du tout.

Cette extension de l'addition est utilisée notamment en théorie de la mesure pour satisfaire l'additivité de la mesure sur des espaces de mesure infinie.

Ordinaux et ensembles ordonnés

La classe des ordinaux étend l'ensemble des entiers naturels par les nombres transfinis. L'addition s'étend ainsi en une opération sur les nombres ordinaux qui est associative mais non commutative. Par exemple, le premier ordinal infini, noté ω, vérifie la relation 1 + ω = ω mais ω < ω + 1.

L'élément 0 reste neutre pour l'addition mais il n'y a pas d'ordinal négatif, bien que l'on puisse définir une différence entre deux ordinaux.

Cette opération s'étend aux ensembles ordonnés en général, l'addition de deux ensembles ordonnés et ayant pour résultat l'union disjointe dans lequel l'ordre des éléments est préservé à l'intérieur de chaque ensemble de départ et tous les éléments de E sont inférieurs à tous les éléments de F.

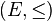
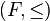
Nombres surréels

Un nombre surréel est une généralisation du concept de nombre sous la forme d'un couple d'ensembles s'écrivant , dans lequel chaque élément de l'ensemble de gauche est plus petit que tout élément de l'ensemble de droite.

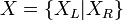
L'addition se formule alors de manière récursive par

avec et .