Système unaire - Définition
Le système unaire aussi appelé système monadique est le système de numération additif le plus simple pour représenter les entiers naturels. Ainsi pour représenter un nombre N, il suffit de répéter N fois un symbole choisi arbitrairement. Par exemple, en utilisant le symbole " | ", le nombre 6 est représenté par " |||||| ". Le fait de compter sur une main est par lui-même un système unaire. Le système unaire est très pratique pour les comptes ou la représentation de résultats, comme des scores de jeux sportifs ou autres, car il ne nécessite pas l'effacement ou le remplacement de l'ancien score.
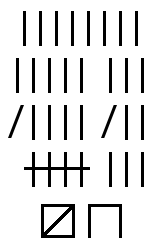
Les marques sont couramment regroupées en groupe de 5 pour améliorer la lisibilité. Cela est similaire à la pratique d'utiliser un séparateur décimal comme un espace ou une virgule dans le système décimal, ce qui permet de rendre les nombres tels que 100.000.000 plus facile à lire. La première ou la cinquième marque dans chaque groupe peut être écrite avec un angle différent des autres pour une meilleure visibilité.
Les additions ou les soustractions sont particulièrement simples dans le système unaire car il s'agit simplement de mettre bout à bout les deux nombres par concaténation. Les multiplications ou divisions sont par contre plus compliquées.
Comparé au système arithmétique positionnel, le système unaire n'est pas très pratique et n'est pas employé en pratique pour des grands calculs.

















































