Addition - Définition

Constructions géométriques

Les nombres intervenant dans une addition représentent parfois des grandeurs géométriques : longueur d'un segment, mesure d'un angle (orienté ou non), aire d'une surface carrée. Dans chacun de ces cas, le calcul de la somme peut être illustré par une construction géométrique à la règle et au compas. Il existe aussi dans chaque cas une construction de la soustraction qui permet à partir de la grandeur somme et d'une des grandeurs de départ de trouver l'autre grandeur de départ.

Longueurs

Pour représenter la somme des longueurs de deux segments, il suffit de prolonger à la règle l'une de ces deux segments au-delà de l'une de ses extrémités, puis de tracer un cercle centré en cette extrémité et ayant pour rayon l'autre longueur. L'intersection du cercle avec le prolongement définit la nouvelle extrémité de la longueur prolongée.

Ce principe est fondamental pour définir ce qu'est un nombre constructible.

Angles géométriques

Étant donnés deux secteurs angulaires tracés dans le plan, il est possible de construire un secteur angulaire dont la mesure de l'angle soit la somme des mesures des angles donnés. Il suffit pour cela de tracer d'abord un triangle isocèle dont le sommet principal et ses côtés adjacents constituent l'un des secteurs angulaires, puis de construire un triangle isométrique de sommet principal à la pointe de l'autre secteur angulaire avec un côté adjacent en commun et l'autre côté à l'extérieur du secteur angulaire. Les deux côtés extérieurs délimitent alors l'angle somme.

En cas d'addition d'angles avec des mesures importantes, l'angle somme peut avoir une mesure de plus de 360°.

Cette procédure, appliquée aux angles d'un triangle, permet de vérifier que la somme des mesures de ces angles vaut bien 180°.

Angles orientés, angles de vecteurs

L'addition d'angles orientés se fait de manière analogue à celle des , à la différence que le premier côté du deuxième angle doit être superposé au deuxième côté du premier angle.

La construction peut alors se décrire en termes de transformations du plan. Si le premier angle orienté est déterminé par un couple de vecteurs représentés à partir de la même origine O et d'extrémités respectives A et B, il suffit de construire l'image B' de B par la rotation de centre O et d'angle le second angle orienté. Les vecteurs de même origine O et d'extrémités A et B' définissent alors l'angle orienté somme.

En appliquant cette opération aux angles de vecteurs de la forme , où M est un point du cercle trigonométrique, l'addition angulaire définit une opération sur les points du cercle qui correspond à la multiplication des nombres complexes de module 1.

Addition des aires de carrés

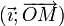
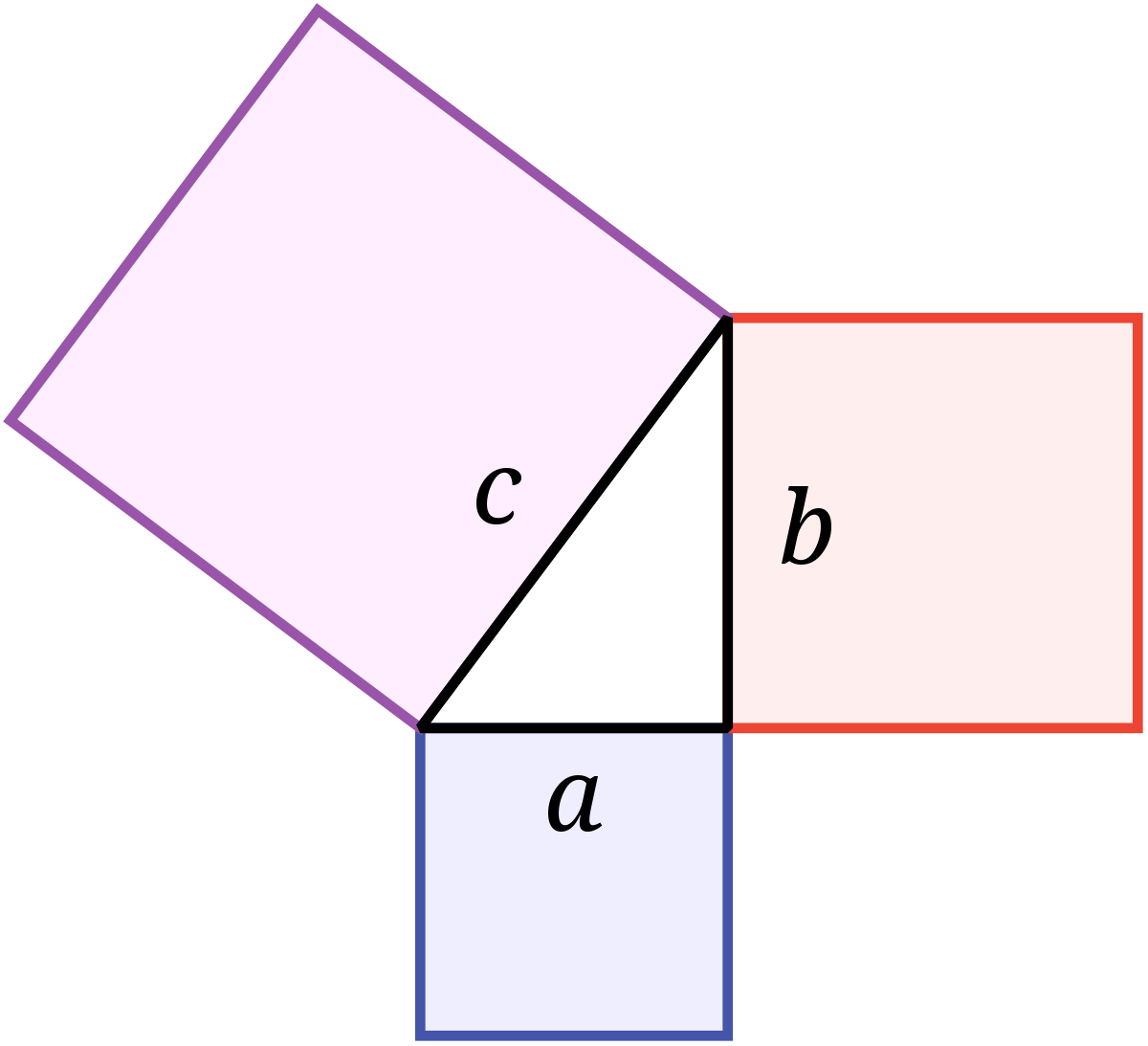
Aires de surfaces carrées

Étant donné deux carrés tracés dans le plan, il est possible de construire un carré dont l'aire est la somme des aires des carrés initiaux. En effet, si les deux carrés initiaux peuvent être tracés de façon à avoir un sommet en commun et deux côtés perpendiculaires, le triangle formé par ces deux côtés est alors un triangle rectangle. Le théorème de Pythagore permet alors de montrer que le carré formé sur le troisième côté du triangle a pour aire la somme des aires des carrés initiaux.

L'opération ainsi définie sur les longueurs des côtés des carrés est l'addition pythagoricienne qui s'exprime (sur les couples de réels positifs) par :

.

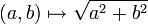
Ce problème de construction généralise celui de la duplication du carré, où les carrés initiaux ont la même dimension.