Notation positionnelle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Numérations selon les cultures | |
|---|---|
| Numération arabo-indienne | |
| arabe khmer indienne | mongole thaï |
| Numérations à l’origine chinoise | |
| chinoise japonaise | à bâtons suzhou |
| Numérations alphabétiques | |
| arménienne cyrillique d'Âryabhata éthiopienne | hébraïque grecque gotique tchouvache |
| Autres systèmes : | |
| attique brahmi champs d'urnes égyptienne étrusque | forestière inuite maya mésopotamienne romaine |
| Notations positionnelles par base | |
| Décimal (10) | |
| 2, 4, 8, 16, 32, 64 | |
| 1, 3, 6, 9, 12, 20, 24, 30, 36, 60, plus… | |
La notation positionnelle est un procédé d'écriture des nombres, dans lequel chaque position est reliée à la position voisine par un multiplicateur, appelé base du système de numération. Chaque position peut être renseignée par un symbole (notation sans base auxiliaire) ou par un nombre fini de symboles (notation avec base auxiliaire). La valeur d'une position est celle du symbole de position ou celle de la précédente position apparente multipliée par la base. Le nombre de symboles nécessaires est au moins égal à la base ou à la plus grande base auxiliaire utilisée. Le système décimal usuel utilise dix symboles, plus les symboles pour les nombres signés et les nombres à virgule, tandis que le système sexagésimal babylonien se sert d'un système décimal auxiliaire pour chaque position.
Systèmes de notation
Plusieurs notations positionnelles, dont certaines hybrides (positionnelles et additives) permettent de représenter les nombres. Voici différentes manières d'écrire le nombre 9018 dans quelques uns de ces systèmes.
Notations hybrides
Les notations hybrides utilisent des symboles représentant les puissance de la base, comme dans les numérations chinoise et japonaise. Ainsi, 十 = 10, 百 = 102, 千 = 103, 万 = 104 dans le système japonais. Ces numérations utilisent, comme pour les puissances de la base, des symboles représentant les sous-puissance de la base. Ainsi, 割 = 10-1, 分 = 10-2, 厘 = 10-3, 毛 = 10-4 dans le système japonais.
- Exemple
9018 s'écrit 九千十八 avec le système utilisé pour la numération japonaise (décimale), soit 9 × 1000 + [1×]10 + 8.
Notations positionnelles et additives
Pour la numération babylonienne, à caractère sexagésimale, les nombres étaient formés de manière additive jusqu'à 60, les valeurs ainsi obtenues étant combinés selon le principe positionnel.
- Exemple
9018 s'écrit
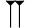
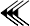
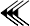

Notations exclusivement positionnelles
- Avec des chiffres formés par une juxtaposition d'éléments
9018 s'écrit :
|
|
|
|
|
|
|
|
avec le système utilisé pour la numération maya (vigésimale, mais irrégulière), soit 1[×7200] + 5[×360] + 0[×20] + 18, ou 1,05,00,18 avec la virgule comme séparateur de positions.
- Avec base auxiliaire
9018 s'écrit 2,30,38 avec le système (sexagésimal) utilisé pour la traduction des textes mésopotamiens, soit 2[×3600] + 30[×60] + 38.
C'est le système utilisé le plus généralement aujourd'hui, avec l'espace comme séparateur, souvent remplacée par le point décimal dans les pays anglosaxons et parfois par une virgule dans les autres pays.
C'est le système utilisé en informatique pour coder les entiers au-dessous d'une certaine taille (dépendant des logiciels et matériels utilisés).
C'est le « décimal codé binaire » utilisé en informatique, principalement dans les applications de comptabilité. Un octet permet de stocker deux chiffres décimaux. Système utilisé non seulement pour éviter des conversions, coûteuses en temps, lors de l'affichage décimal des nombres, particulièrement pour ceux de grande taille, mais aussi pour éviter les imprécisions que pourrait occasionner la représentation logarithmique des grands nombres dans la notation dite scientifique.
- Sans base auxiliaire, sans zéro
9018 s'écrit 8X18 dans le système positionnel expérimental sans zéro (décimal), soit 8[×1000] + 10[×100] + 1[×10] + 8, ou 8,10,1,8, avec la virgule comme séparateur de positions.
- Sans base auxiliaire, avec zéro
9018 s'écrit ๙๐๑๘ avec le système utilisé pour la numération thaï (décimale), soit 9[×1000] + 0[×100] + 1[×10] + 8, ou 9018, de même qu'avec nos chiffres arabo-indiens.





















































