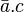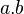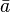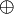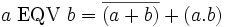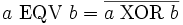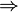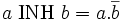Algèbre de Boole (logique) - Définition

Arbre d'expression

Les expressions logiques sont souvent représentées en informatique sous forme d'arborescence. Cette dernière comporte un sommet (la racine en fait) auquel sont rattachés différents sous-arbres (ou branches). Les bifurcations sont des sommets internes. Le nombre de sous-arbres reliés à un même sommet est appelé arité. Les sommets sans issue sont appelés feuilles. Chaque sommet interne est identifié par un opérateur booléen alors que les feuilles représentent les variables qui subissent ces opérations.

Fonctions logiques

Mathématiquement, une fonction logique ou opérateur logique est une application de Bⁿ dans B.

En électronique, une fonction logique est une boîte noire qui reçoit en entrée un certain nombre de variables logiques et qui rend en sortie une variable logique dépendant des variables d'entrée. L'article fonction logique précise comment construire les boîtes noires de quelques fonctions fondamentales.

Une table de vérité permet de préciser l'état de la sortie en fonction des états des entrées.

On démontre que toute fonction logique peut se décrire à l'aide des trois opérations de base.

• 
• 
• 

Fonctions logiques fondamentales

Elles sont issues des trois opérations de base et définissent alors

• une fonction de B dans B : le complémentaire ou inversion
• deux fonctions de B² dans B qui sont la somme (ou OU) et le produit (ou ET)

Table de vérité de l'inverse
a
0	1
1	0

Table de vérité de la somme
a	b	a b
0	0	0
0	1	1
1	0	1
1	1	1

Table de vérité du produit
a	b	a b
0	0	0
0	1	0
1	0	0
1	1	1

Fonctions logiques composées

Ce sont les fonctions logiques à deux variables. Parmi celles-ci, on en dénombre certaines suffisamment intéressantes pour qu'on leur donne un nom.

Disjonction exclusive

Le OU étudié jusqu'à présent doit se comprendre de la manière suivante : « l'un ou l'autre ou les deux ». Il est également appelé « OU inclusif ». Le OU exclusif (ou XOR pour ' eXclusive OR') s'entend comme : « l'un ou l'autre, mais pas les deux ».

Il se compose de la manière suivante :

Table de vérité de XOR
a	b	a b
0	0	0
0	1	1
1	0	1
1	1	0

Le « ou exclusif » est parfois noté par le signe arithmétique (différent de). Fonctionnellement, on utilise aussi un + entouré: .

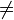
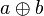
Équivalence

L'équivalence (notée EQV) est vraie si les deux entrées ont la même valeur et fausse sinon. Elle est appelée aussi « non-(ou exclusif) » (ou encore « et inclusif » ). Elle se compose comme suit :

On peut aussi dire que :

Table de vérité de EQV
a	b	a b
0	0	1
0	1	0
1	0	0
1	1	1

Il arrive que l'équivalence soit notée par le signe , bien que ce choix ne soit pas recommandé compte-tenu des autres sens possibles attachés à ce signe.

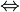
Elle peut aussi être notée "==" dans certains langages (C, C++, PHP…).

Implication

L'implication (notée IMP) s'écrit de la manière suivante :

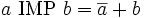
Cette opération n'est pas commutative. a est une condition suffisante pour b, qui, elle, est une condition nécessaire pour a.

Mais

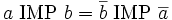
Illustration : de l'affirmation

"S'il fait beau, j'irai me promener."

on peut conclure

"Si je ne vais pas me promener, il ne fait pas beau."

mais on ne peut pas en déduire

"S'il ne fait pas beau, je ne vais pas me promener."

car on ne sait pas si je n'aime pas me promener aussi sous la pluie.

Table de vérité de IMP
a	b	a b
0	0	1
0	1	1
1	0	0
1	1	1

Inhibition

L'inhibition (notée INH) se compose comme suit :

Cette opération n'est pas commutative.

Table de vérité de INH
a	b
0	0	0
0	1	0
1	0	1
1	1	0

Exemple de fonctions logiques à trois ou quatre variables

Fonction logique à trois variables

Si l'on reprend l'exemple du téléphone, on se trouve en présence de 3 variables :

• a = "le téléphone sonne"
• b = "on a envie de répondre"
• c = "on a envie d'appeler quelqu'un"

la variable d = "on décroche" est fonction logique des 3 précédentes. On écrira que

d = a.b + c

car on décroche quand ça sonne et qu'on a envie de répondre ou quand on a envie d'appeler quelqu'un.

La table de vérité de cette fonction d est alors la suivante :

Table de vérité de décrocher
a	b	c	d
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

L'observation de la table montre que notre analyse première comportait une situation absurde: le téléphone sonne, on a envie d'appeler quelqu'un, mais on n'a pas envie de répondre et on décroche quand même. Cela n'est certainement pas le comportement souhaité, il est donc préférable de modifier la fonction décrocher de façon à ce qu'on obtienne le tableau suivant:

Table de vérité de décrocher2
a	b	c	d2
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

En lisant le procédé de la simplification des expressions ci-dessous, on voit que la formule de décrocher2 correspond à .

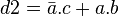
Fonction logique à quatre variables

Un bon élève s'interroge s'il est sage de sortir un soir. Il doit décider en fonction de quatre propositions :

• a = il a assez d'argent
• b = il a fini ses devoirs
• c = le transport en commun est en grève
• d = l'auto de son père est disponible

Cet élève pourra sortir si :

• il a assez d'argent, a = vrai
• il a fini ses devoirs, donc b = vrai
• le transport en commun n'est pas en grève, donc c = faux
• ou si l'auto de son père est disponible, donc d = vrai

Donc l'expression logique de sortir en fonction de l'état des variables a, b, c et d ; et elle peut s'écrire ainsi :

Sortir =

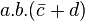
Minimisation d'une expression

Une fonction logique peut être déterminée

• soit sous forme d'une expression faisant intervenir les 3 opérations ( , , )
• soit sous forme de sa table de vérité. Dans ce cas il sera toujours possible d'écrire cette fonction comme une somme de produits.

Exemple: Dans l'exemple de "téléphoner2", on s'aperçoit que le résultat est à 1 quand (a, b, c) = (0, 0, 1) ou (0, 1, 1) ou (1, 1, 0) ou (1, 1, 1).

Cela permet de définir d2 par

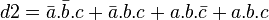
Il est alors intéressant de trouver une expression minimisant le nombre de termes et le nombre de lettres dans chaque terme. C'est l'objectif de certaines techniques comme la méthode de Quine-Mc Cluskey, les diagrammes de Karnaugh…

Exemple (suite) : la somme précédente peut être réduite en

par factorisation des deux premiers termes par et factorisation des deux derniers termes par