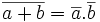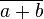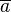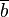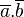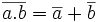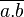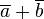Algèbre de Boole (logique) - Définition

Introduction

L'algèbre de Boole, ou calcul booléen, est la partie des mathématiques, de la logique et de l'électronique qui s'intéresse aux opérations et aux fonctions sur les variables logiques. Plus spécifiquement, l'algèbre booléenne permet d'utiliser des techniques algébriques pour traiter les expressions à deux valeurs du calcul des propositions. Elle fut initiée par le mathématicien britannique du milieu du XIX^e siècle George Boole.

Aujourd'hui, l'algèbre de Boole trouve de nombreuses applications en informatique et dans la conception des circuits électroniques. Elle fut utilisée la première fois pour les circuits de commutation téléphoniques par Claude Shannon.

L'algèbre de Boole des fonctions logiques permet de modéliser des raisonnements logiques, en exprimant un « état » en fonction de conditions. Par exemple :

Communication = Émetteur ET Récepteur

Communication est « VRAI » si Émetteur actif ET Récepteur actif (c'est une fonction logique dépendant des variables Émetteur et Récepteur)

Décrocher = ( Décision de répondre ET Sonnerie ) OU décision d'appeler

Décrocher est « VRAI » si on entend la sonnerie ET que l'on décide de répondre OU si l'on décide d'appeler.

L'algèbre de Boole étant un domaine commun à trois disciplines, on rencontre des notations différentes pour désigner un même objet. Dans le reste de l'article, on indiquera les diverses notations, mais on en privilégiera une pour conserver une certaine homogénéité.

Algèbre de Boole des valeurs de vérité

On appelle B l'ensemble constitué de deux éléments appelés valeurs de vérité {VRAI, FAUX}. Cet ensemble est aussi noté

• B = {1, 0}
• B = .

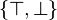
On privilégiera dans la suite la notation B = {1, 0}.

Sur cet ensemble on peut définir deux lois (ou opérations ou foncteurs), les lois ET et OU et une transformation appelée complémentaire, inversion ou contraire.

Conjonction

Elle est définie de la manière suivante : a ET b est VRAI si et seulement si a est VRAI et b est VRAI. Cette loi est aussi notée

• 
• 
• « & » ou « && » dans quelques langages de programmation (Perl, C, PHP...)
• « AND » dans certains langages de programmation (Ada, Pascal, Python, PHP ...)
• « ∧ » dans quelques notations algébriques, ou en APL

On privilégiera dans la suite la notation

On peut construire la table de cette loi (comme une table d'addition ou de multiplication de notre enfance) mais on ne la confondra pas avec une table de vérité.

Table de la loi ET
b\a	0	1
0	0	0
1	0	1

Disjonction

Elle est définie de la manière suivante : a OU b est VRAI si et seulement si a est VRAI ou b est VRAI. (si a est vrai et que b est vrai aussi, alors a OU b est vrai.) Cette loi est aussi notée

• 
• 
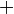
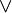
• « | » ou « || » dans quelques langages de programmation
• « OR » dans certains langages de programmation
• « ∨ » dans quelques notations algébriques ou en APL.
• « < » très rarement.

On privilégiera dans la suite la notation mais on prendra garde que cette loi n'est pas l'addition usuelle dans Z/2Z. C'est pourquoi, en mathématiques et en logique mathématique, cette notation n'est pas utilisée pour désigner le "ou inclusif" : elle est réservée au "", opération qui (jointe au "et") fait de toute algèbre de Boole un anneau de Boole, en particulier une Z/2Z-algèbre (d'où le nom d'algèbre de Boole).

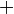
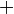
Table de la loi OU
b\a	0	1
0	0	1
1	1	1

Négation

Le contraire de "a" est VRAI si et seulement si a est FAUX. Le contraire de a est noté

• non-a
• 
• 
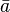
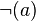
• « ! » dans quelques langages de programmation (C, C++, ...)
• « NOT » dans certains langages de programmation (ASM, ...)
• « ~ » dans quelques notations algébriques, en APL et dans quelques langages d'interrogation de bases de données (Sql, ...).

On privilégiera dans la suite la notation .

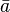
On obtient alors et

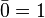
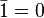
Propriétés

Associativité

Comme avec les opérations habituelles, certaines parenthèses sont inutiles:
(a + b) + c = a + (b + c) = a + b + c
(a.b).c = a.(b.c) = a.b.c

Commutativité

L'ordre est sans importance:
a + b = b + a
a.b = b.a

Distributivité

Comme avec les opérations habituelles, il est possible de distribuer :
a.(b + c) = a.b + a.c
Attention : comportement différent par rapport aux opérateurs + et * habituels :
a + (b.c) = (a + b).(a + c)

Idempotence

a + a + a + [...] + a = a
a.a.a.[...].a = a

Élément neutre

a + 0 = a
a.1 = a

Élément nul

0.a = 0
1 + a = 1

Absorption

a + a.b = a
a.(a + b) = a

Simplification

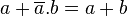
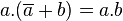
Redondance

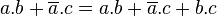
Complémentarité

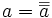
(« La lumière est allumée » = « la lumière n'est pas non allumée »)

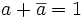
(« VRAI » SI lumière_allumée OU SI lumière_non_allumée → c'est toujours le cas → vrai dans tous les cas → toujours VRAI, donc =1)

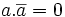
(« VRAI » SI lumière_allumée ET SI lumière_non_allumée → impossible → faux dans tous les cas → toujours FAUX donc =0)

Structure

On retrouve alors toutes les propriétés qui confèrent à B une structure d'algèbre de Boole

Priorité

Pour faciliter leur compréhension, il a été décidé que ces opérations seraient soumises aux mêmes règles que les opérations « de tous les jours », la fonction ET (multiplication logique) est ainsi prioritaire par rapport à la fonction OU (somme logique) ; on peut, pour s'aider, placer des parenthèses dans les opérations.

Exemple :

a = 0;b = 1;c = 1

On cherche a.b + c = ???

D'abord on calcule a.b :

a.b = 0.1

0.1 = 0

Puis, on calcule 0 + c :

0 + c = c

c = 1

Le résultat final est donc:

a.b + c = (a.b) + c = 1

Théorème de De Morgan

Fonction	Table de vérité/Table de fonctionnement
	a b a+b 0 0 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0

Dans les deux cas, l'expression ne sera VRAIE que si a et b sont fausses.

Fonction	Table de vérité/Table de fonctionnement
	a b a.b 0 0 0 1 1 1 1 0 1 0 1 1 0 1 1 0 0 1 0 1 1 1 1 1 0 0 0 0

Dans les deux cas, l'expression ne sera FAUSSE que si a et b sont vraies.