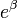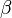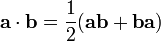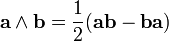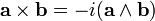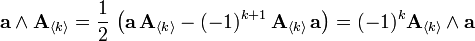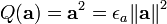Algèbre géométrique (structure) - Définition

Produits intérieur et extérieur

Le produit scalaire usuel et le produit vectoriel de l'algèbre vectorielle traditionnelle (sur ) trouvent leurs places dans l'algèbre géométrique comme le produit interne

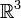
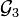
(qui est symétrique) et le produit externe

avec

(qui est antisymétrique). La distinction entre vecteurs axiaux et polaires, obscure en algèbre vectorielle, est naturelle en algèbre géométrique, où elle s'exprime comme la distinction entre vecteurs et bivecteurs (éléments de degré deux). Le i ici est l'unité pseudoscalaire du 3-espace euclidien, qui établit une dualité entre les vecteurs et les bivecteurs, et est nommé ainsi à cause de la propriété prévue .

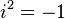
Alors que le produit vectoriel peut seulement être défini dans un espace à trois dimensions, les produits interne et externe peuvent être généralisés à n'importe quelle dimension.

Soient un vecteur et un multivecteur homogène de degré k. Leur produit interne est alors : et leur produit externe est

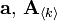
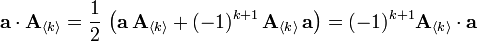
La règle de contraction

La connexion entre les algèbres de Clifford et les formes quadratiques provient de la propriété de contraction. Cette règle donne aussi à l'espace une métrique définie par le produit interne naturellement dérivé. Également, dans l'algèbre géométrique dans toute sa généralité, il n'existe pas une quelconque restriction sur la valeur du scalaire, il peut être négatif, même zéro (dans ce cas, la possibilité d'un produit interne est éliminée si vous demandez ).

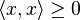
La règle de contraction peut être mise sous la forme :

où est le module du vecteur a et est appelé la signature du vecteur a. Ceci est particulièrement utile dans la construction de l'espace de Minkowski (l'espace-temps de la relativité) via . Dans ce contexte, les vecteurs nuls sont appelés "vecteurs de lumière", les vecteurs à signature négative sont appelés "vecteurs d'espace" et les vecteurs à signature positive sont appelés "vecteurs de temps" (ces deux dernières dénominations sont échangées lorsqu'on utilise à la place).

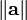
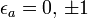
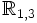
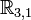
Histoire

L'algèbre géométrique de David Hestenes et al. (1984) réinterprête les algèbres de Clifford sur les réels et son objectif est de revenir au nom et à l'interprétation que Clifford avait originellement prévus. L'ouvrage d'Emil Artin Geometric Algebra discute des algèbres associées avec chacune des nombreuses géométries, dont la géométrie affine, la géométrie projective, la géométrie symplectique et la géométrie orthogonale.

Applications de l'algèbre géométrique

Un exemple utile est , et la façon dont il engendre , un exemple d'algèbre géométrique appelé algèbre de l'espace-temps par Hestenes. Le champ tensoriel électromagnétique, dans ce contexte, devient juste un bivecteur où l'unité imaginaire est l'élément de volume, donnant un exemple de réinterprétation géométrique de "tours" traditionnels.

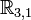
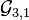
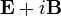
Les accélérations dans cet espace métrique lorentzien ont la même expression que la rotation dans l'espace euclidien, où est bien sûr le bivecteur engendré par le temps et les directions d'espace impliquées, considérant dans le cas euclidien que c'est le bivecteur engendré par les deux directions d'espace, renforçant l'"analogie" de la quasi-identité.