Algèbre géométrique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

En mathématiques, l’algèbre géométrique regroupe des méthodes géométriques, utilisées par les grecs de l'antiquité, pour établir des résultats maintenant classés dans la branche mathématique appelée algèbre. Ces techniques permettent la mise en évidence des propriétés élémentaires de la multiplication, d’effectuer des calculs comme la somme des premiers nombres entiers, ou impairs. Elles permettent d’établir des résultats comme des identités remarquables ou de résoudre une équation du second degré. L’algèbre géométrique fournit aussi des méthodes de résolution plus complexes, comme celles qui montrent l’existence de nombres irrationnels.
Si ces méthodes sont anciennes et correspondent à une vision des mathématiques qui n'est plus la notre, elles sont toujours utilisées dans l’enseignement, soit pour donner des preuves simples de certains résultats, soit pour développer une conscience intuitive de résultats qu'une présentation algébrique rendrait plus abstraits.
Le terme « algèbre géométrique » provient d’un livre de l’historien des sciences Hieronymus Georg Zeuthen , écrit en 1902. Il est popularisé par Paul Tannery l'année suivante. Les livres II et VI des Éléments d'Euclide en forment le cœur. Si une lecture contemporaine permet d'interpréter de manière algébrique les résultats démontrés ainsi, tel n'était néanmoins pas la lecture des grecs qui n'avaient pas découvert les principes fondateurs de l'algèbre. Pour cette raison, cette lecture apocryphe de la science grecque est parfois critiquée.
L'expression « algèbre géométrique » est aussi utilisée en mathématiques pures, elle correspond alors à un concept moins élémentaire. Elle désigne une branche contemporaine des mathématiques consistant à associer une géométrie à une structure d'algèbre. Cet aspect est traité dans l'article Algèbre géométrique (structure). Les termes géométrie algébrique désignent une branche différente des mathématiques, constituée d'un savoir essentiellement acquis au XIXe siècle et XXe siècle et toujours d'actualité en recherche mathématiques. Ces terme désignent alors l'approche opposée, consistant à utiliser des techniques algébriques pour résoudre des problèmes de géométrie.
Propriétés de la multiplication
Nombre entier positif
On peut remarquer que 4 x 3 est égal à 3 x 4 et, de manière plus générale « le produit de nombres entiers ne dépend pas de l’ordre des facteurs ».
Pour se persuader de l’exactitude de ce résultat, on peut considérer des petits carrés, tous de même dimension, assemblés en rangées de 3. En accolant verticalement 4 rangées de 3, on obtient un rectangle de base 4 cotés de petits carrés et de hauteur 3. Ce rectangle, illustrée sur la figure de gauche, contient 4 x 3 = 12 petits carrés. Appliquer un quart de tour au rectangle ne modifie pas le nombre de petits carrés le composant, ce qui montre que le résultat de 4 x 3 correspond au nombre de petits carrés composant le rectangle associé à l’opération 3 x 4. Ce résultat ne dépend pas des valeurs 3 et 4, on peut choisir deux nombres entiers quelconques que l’on peut noter a et b. L’égalité, qui s’écrit de la manière suivante, traduit se que l’on appelle la commutativité de la multiplication :

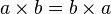
La commutativité de la multiplication n’est pas l’unique propriété s’illustrant à l’aide de la géométrie. La figure de droite peut se lire de deux manières différentes. Tout d’abord, le grand rectangle est la somme des aires des rectangles bleus et rouges. Le raisonnement précédent montre que son aire est égale à 9 x 3 + 9 x 4. On peut le voir aussi comme un unique rectangle, s'il l'on ne tient pas compte des couleurs, d’aire égale à 9 x (3 + 4). Ces deux écritures correspondent donc au même nombre. Une fois encore, le résultat est vrai non seulement pour les nombres 9, 3 et 4, mais aussi pour n’importe quel ensemble de trois nombres, que l’on peut noter a, b et c. On obtient le résultat suivant, appelé distributivité de la multiplication par rapport à l’addition.
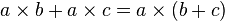
Ainsi, l'usage de la géométrie et plus spécifiquement le calcul des aires permet d'établir certaines propriétés de la multiplication. Ce principe est la base de l'algèbre géométrique.
Fraction
Pour faire de la géométrie, les nombres entiers ne suffisent pas toujours. Une longueur peut être égale à la moitié d'une autre. Les grecs ont donc été amenés à établir les règles opératoires régissant les fractions. Une fois encore le calcul des aires est utile. Pour illustrer cette approche, cherchons à additionner 1/6 et 4/9. Considérons pour cela un rectangle dont l’aire est égale à 1. On choisit deux quadrillages qui décomposent le rectangle en petits rectangles identiques. On choisit ces quadrillages compatibles, c'est-à-dire que la superposition des quadrillages est encore un quadrillage en petits rectangles tous identiques, comme l’illustre la figure ci-dessous :
La première représentation du rectangle montre que la fraction 1/6 est représentée par un quadrillage découpant le rectangle en 6 petits rectangles, la superposition des quadrillages en crée 18 et 1/6 = 3/18. On obtient finalement les égalités :
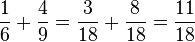
D'une manière générale, si a, b, c, et d sont des nombres entiers tels que ni b ni d ne sont nuls, alors :
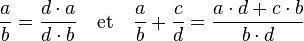
L’article détaillé montre comment la démarche permet de déterminer toutes les règles opératoires des fractions.