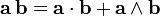Algèbre géométrique (structure) - Définition

Introduction

En mathématiques, une algèbre géométrique est une algèbre multilinéaire avec une interprétation géométrique (le terme est aussi utilisé dans un sens plus général pour décrire l'étude et l'application de ces algèbres : l'algèbre géométrique est l'étude des algèbres géométriques). Officieusement, une algèbre géométrique est une algèbre de Clifford qui inclut un produit géométrique.

L'algèbre géométrique est utile dans les problèmes de physique qui impliquent des rotations, des phases ou des nombres imaginaires. Les partisans de l'algèbre géométrique disent qu'elle fournit une description plus compacte et intuitive de la mécanique quantique et classique, de la théorie électromagnétique et de la relativité. Les applications actuelles de l'algèbre géométrique incluent la vision par ordinateur, la biomécanique ainsi que la robotique et la dynamique des vols spatiaux.

Le produit géométrique

Une algèbre géométrique est une algèbre construite sur un espace vectoriel dans lequel un produit géométrique est défini. Les éléments de l'algèbre géométrique sont des multivecteurs. Le produit géométrique possède les propriétés suivantes, pour tous les multivecteurs  :

1. Clôture
2. Distributivité sur l'addition des multivecteurs :
   • 
   • 
3. Associativité
4. Elément unité (scalaire) :
   • 
5. Contraction tensorielle : pour tout "vecteur" (un élément de degré un) est un scalaire (nombre réel)
6. Commutativité du produit par un scalaire :
   • 

Les propriétés (1) et (2) sont parmi celles nécessaires pour une algèbre sur un corps. (3) et (4) signifient qu'une algèbre géométrique est une algèbre associative unitaire.

Le point distinctif de cette formulation est la correspondance naturelle entre les entités et les éléments de l'algèbre associative. Ceci provient du fait que le produit géométrique est défini en termes de produit vectoriel et produit scalaire de vecteurs comme

L'espace vectoriel original est construit sur les nombres réels comme scalaires. Dorénavant, un vecteur est quelque chose dans lui-même. Les vecteurs seront représentés par des symboles en minuscules grasses.

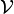
La définition et l'associativité du produit géométrique nécessitent le concept d'inverse d'un vecteur (ou division par un vecteur). Ainsi, on peut facilement établir et résoudre des équations algébriques vectorielles qui autrement seraient encombrantes à manipuler. De plus, on gagne une signification géométrique qui serait difficile à rechercher, par exemple, en utilisant les matrices. Malgré le fait que tous les éléments ne sont pas inversibles, le concept d'inversion peut être étendu aux multivecteurs. L'algèbre géométrique permet que l'on traite des sous-espaces directement, ainsi que leur manipulation. En outre, l'algèbre géométrique est un formalisme sans coordonnées.

Les objets géométriques comme sont appelés des bivecteurs. Un bivecteur peut être décrit comme un segment plan (un parallélogramme, un cercle etc.) doté d'une orientation. Un bivecteur représente tous les segments planaires avec la même grandeur et direction, quel que soit l'endroit où ils se trouvent dans l'espace qui les contient. Néanmoins, une fois que soit le vecteur ou est signifié à partir d'un certain point préféré (e.g. dans les problèmes de physique), le plan orienté est déterminé sans ambiguïté.

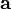
Comme exemple significatif, bien que simple, on peut considérer un vecteur différent de zéro , à partir d'un point choisi comme origine, dans l'espace euclidien usuel, . L'ensemble de tous les vecteurs , B désignant un bivecteur donné contenant , détermine une ligne l parallèle à . Puisque B est une aire orientée, l est uniquement déterminé en conservant l'origine choisie. L'ensemble de tous les vecteurs , s désignant un scalaire (réel) donné, détermine un plan P orthogonal à . De nouveau, P est uniquement déterminé en conservant l'origine choisie. Les deux morceaux d'information, B et s, peuvent être établis indépendamment l'un de l'autre. Maintenant, quel est le vecteur qui satisfait le système { , } ? Géométriquement, la réponse est claire : c'est le vecteur qui part de l'origine et aboutit à l'intersection de l et P. Par l'algèbre géométrique, même la réponse algébrique est simple : ^-1, où l'inverse d'un vecteur différent de zéro est exprimé par ^-1 . Note : La division par un vecteur transforme le multivecteur s + B en une somme de deux vecteurs. De plus, la structure de la solution ne dépend pas de l'origine choisie.

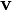
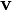
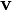
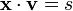
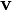
Tel qu'il est défini, le produit externe (ou produit extérieur, ou produit vectoriel) engendre l'algèbre graduée (algèbre extérieure de Hermann Grassmann) des multivecteurs. Un multivecteur est ainsi une somme directe d'éléments de degré k (k-vecteurs), où k va de 0 (scalaires) à n, la dimension de l'espace vectoriel original . Les multivecteurs sont représentés ici par les majuscules grasses. Note : Les scalaires et les vecteurs deviennent des cas particuliers de multivecteurs ("0-vecteurs" et "1-vecteurs", respectivement).