Géométrie symplectique - Définition

Introduction

La géométrie symplectique est un domaine actif de la recherche mathématique, né de la volonté d'une formulation mathématique naturelle à la mécanique classique. Elle est à la rencontre de la géométrie différentielle et des systèmes dynamiques. En mathématiques, elle trouve des applications en géométrie algébrique, en géométrie riemannienne et en géométrie de contact. Formellement, elle est définie comme l'étude des « 2-formes différentielles fermées non dégénérées » — appelées formes symplectiques — sur les variétés différentielles.

Étymologie, histoire de la terminologie

L'adjectif symplectique fut introduit par le mathématicien Hermann Weyl pour désigner le groupe symplectique Sp(2n), le groupe des automorphismes linéaires réels de Cⁿ conjuguant la multiplication par i à elle-même. Ce groupe était appelé « groupe du linéaire complexe » et une confusion était possible avec le groupe des automorphismes linéaires complexes. Hermann Weyl justifie son choix :

« 

The name “complex group” formerly advocated by me in allusion to line complexes, as these are defined by the vanishing of antisymmetric bilinear forms, has become more and more embarrassing through collision with the word “complex” in the connotation of complex number. I therefore propose to replace it by the corresponding Greek adjective “symplectic”.
(Le nom « groupe complexe » que j'ai précédemment évoqué en allusion à la droite complexe, est devenu de plus en plus embarrassant par l'usage de « complexe » dans l'expression « nombre complexe ». Je propose donc de le remplacer par l'adjectif grec correspondant « symplectique ».)

 »

— Hermann Weyl, The classical Groups. Their Invariants and Representations

Plus exactement, l'adjectif « symplectique » est basé sur la racine grecque συµπλεκτικoς, traduction de la racine latine de complexus. La racine latine a donné le nom de complexité d'où dérive « nombre complexe », ce nom latin traduit l'idée d'entrelacement. En histoire naturelle, l'adjectif symplectique désigne « être entrelacé avec un autre corps ».

Par extension, l'adjectif symplectique a été utilisé dans l'appellation de forme symplectique et de variété symplectique (voir définitions ci-dessous).

Symétries en mécanique

Le deuxième argument confortant l'idée que la géométrie symplectique est la géométrie naturelle des espaces de phases est la facilité avec laquelle elle permet d'intégrer les questions de symétrie et leurs conséquences dans la théorie.

Théorème de Noether

La présence de symétries dans un système mécanique a toujours pour conséquence la conservation de certaines quantités calculées à partir des positions et vitesses des objets étudiés. Ainsi lorsqu'un système est invariant par translation dans une direction, la quantité de mouvement dans cette direction est conservée. Lorsque le système est invariant par rotation autour d'un axe, le moment cinétique par rapport à cet axe est conservé.

Dans la formulation Newtonnienne de la mécanique classique, il semble impossible d'énoncer un théorème général qui engloberait les exemples cités ainsi que des situations possédant des symétries plus compliquées.

Le théorème de Noether affirme que dès que l'on a un groupe à un paramètre de transformations qui préserve un système mécanique il existe une quantité conservée lors de l'évolution de ce système. En fait l'énoncé complet donne une formule pour cette quantité en fonction des transformations et du système considérés.

Dans la formulation lagrangienne de la mécanique on peut démontrer ce théorème en un dizaine de lignes. Dans la formulation hamiltonienne en termes de géométrie symplectique la démonstration ne fait qu'une ligne et l'énoncé se généralise au cas de groupe de transformations à un nombre quelconque de paramètres qui ne commutent pas nécessairement entre elles. Le nombre de quantités conservées est alors égal au nombre de paramètres du groupe de transformations.

Systèmes hamiltoniens intégrables

Une des conséquences de l'existence de quantités conservées est qu'elle contraint le système mécanique étudié à rester dans certaines régions de l'espace des phases définies par les conditions initiales.

Lorsqu'on a autant de quantités conservées que de degrés de liberté on dit que le système mécanique est intégrable et la situation devient très simple, c'est ce qu'affirme le théorème d'Arnold-Liouville : pour presque toute énergie de départ il existe des coordonnées et des nombres tels que

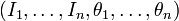
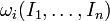
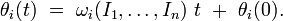
Systèmes presque intégrables

Bien sûr la plupart des systèmes mécaniques ne sont pas intégrables mais certains sont proches d'être intégrables, on peut alors essayer de comprendre dans quelle mesure leur comportement s'éloigne de celui d'un système intégrable, c'est l'objet de la théorie des perturbations qui fait elle aussi un grand usage de la structure symplectique des espaces de phases.

Des connaissances élémentaires en géométrie différentielle sont nécessaires pour aborder les aspects techniques de la géométrie symplectique. L'introduction ici présentée donne un entr'aperçu des résultats fondamentaux qui se veut abordable.

La géométrie symplectique partage de nombreux points communs avec la géométrie de Riemann, qui étudie les variétés différentielles dotées de tenseurs bilinéaires non dégénérés symétriques. Par contre, les variétés symplectiques n'ont pas d'invariants locaux telle que la courbure. C'est une conséquence du théorème de Darboux qui établit que deux variétés symplectiques sont localement isomorphes. La question de savoir quelles variétés admettent des structures symplectiques n'est pas encore complètement résolue.

Chaque variété de Kähler est également une variété symplectique. Au cours des années 1970, les experts du domaine étaient incertains quant à la question de savoir si des variétés symplectiques compactes autres que celles de Kähler existaient, mais depuis plusieurs exemples ont peu être construits (le premier est dû à William Thurston).

La plupart des variétés symplectiques ne sont pas de Kähler et n'ont donc pas de structure complexe intégrable compatible avec la forme symplectique. Mikhaïl Gromov a remarqué cependant que les variétés symplectiques possèdent de nombreuses structures quasi-complexes qui vérifient tous les axiomes d'une variété complexe à l'exception du fait que les fonctions de transition n'y sont pas holomorphes.

Gromov développa le fait qu'il existe de telles structures pour fonder une théorie des courbes pseudoholomorphes, qui permit de grandes avancées dans la recherche géométrique symplectique, et notamment la découverte d'une classe d'invariants connus sous le nom d'invariants de Gromov-Witten, en coopération avec Edward Witten, qui jouent un rôle clé dans la théorie des cordes.