Application affine - Définition
La liste des auteurs de cet article est disponible ici.
Transformation affine comme cas particulier d'homographie
L'espace affine


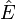

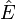

Réciproquement, toute homographie laissant un hyperplan invariant se restreint dans le complémentaire de cet hyperplan à une transformation affine.
En raccourci, les transformations affines sont les homographies ayant un hyperplan invariant, et on en déduit que le groupe affine est un sous-groupe du groupe projectif.
Caractérisations géométriques des applications affines
On suppose dans ce paragraphe que
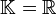
1) Les applications affines sont les applications conservant les barycentres.
Ceci vaut aussi bien pour les barycentres de familles finies que des centres d'inertie de parties munies de fonctions de masse ; le centre d'inertie d'un objet aura pour image par une application affine le centre d'inertie de l'objet image.
Grâce à l'associativité, on peut réduire la condition au fait de conserver les barycentres de deux points, mais on ne peut aller jusqu'à la conservation des milieux : les applications conservant les milieux sont les applications



Cependant, on peut montrer que
2) Les applications affines sont les applications continues conservant les milieux.
Remarque : la propriété de conservation des milieux équivaut à celle de conservation des parallélogrammes.
3) En dimension
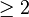
Ceci est une version du théorème fondamental de la géométrie affine. Il est remarquable qu'il n'y ait pas besoin de préciser que deux droites parallèles ont des images parallèles.
On peut même restreindre la caractérisation à :
4) En dimension
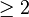
Voir la page théorème fondamental de la géométrie affine pour plus de précisions.

















































