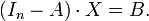Application affine - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
C’est Euler, en 1748, qui est à l’origine du terme « transformation affine », car dit-il, « deux courbes images l’une de l’autre par une telle transformation présentent entre elles une certaine affinité ».
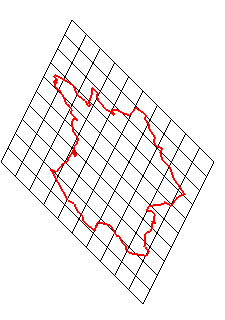
De nos jours, une application affine est une application entre deux espaces affines qui préserve la structure affine, c'est-à-dire qui envoie les droites, plans, espaces,... en des droites, plans, espaces, ... tout en préservant la notion de parallélisme.
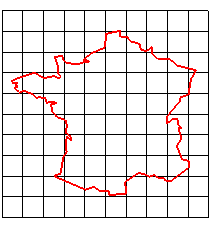 ➪
➪ 
Définition et premières propriétés
Une application
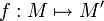

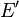
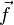
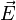

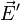
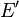

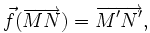
pour tous points

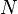

Une application affine est donc déterminée par la donnée d'un couple de points homologues
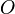
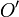
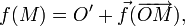
Si E est de dimension n, elle est également déterminée par la donnée de n + 1 points formant un repère affine et de leurs images.
Définitions équivalentes :
- Application linéaire d'un vectorialisé
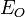

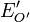
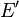
- Application conservant les barycentres.
Deux sous-affines parallèles dans

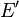
Une application affine d'un espace affine dans lui même est appelée endomorphisme affine, et un endomorphisme bijectif est appelé un automorphisme, ou plus couramment une transformation affine. Les transformations affines forment un groupe, appelé le groupe affine de

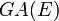
Points fixes des endomorphismes affines
Les points fixes jouent un rôle important pour les endomorphismes affines car un endomorphisme affine ayant un point fixe
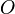
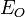
S'il est non vide, l'ensemble des points fixes de l'endomorphisme affine

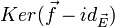
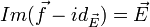



D'autre part, pour un endomorphisme affine



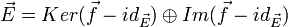
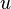
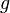
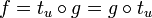
Exemples d'endomorphismes affines
- les translations (caractérisation : partie linéaire = l'identité).
- les symétries centrales (caractérisation : partie linéaire = - l'identité) .
- plus généralement, les homothéties (affines) (caractérisation : partie linéaire = une homothétie (vectorielle), uniquement dans le cas d'un rapport différent de 1)
- les symétries (affines) (caractérisation : au moins un point fixe et partie linéaire = une involution, ou application affine de carré égal à l'identité)
- les projections (affines) (caractérisation : au moins un point fixe et partie linéaire = un projecteur, ou application affine de carré égal à elle-même)
- les affinités, comprenant toutes les précédentes
- les transvections
- dans le cas euclidien : les isométries et similitudes
Les applications affines dans Kn
Les applications affines dans

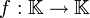
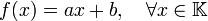
avec


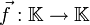
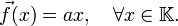
De façon plus générale, une application affine
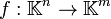
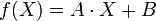
où
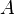
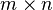
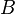
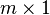
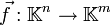
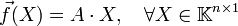
Translations et affinités dans Rn
- L'application T est une translation de vecteur
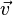

- L'application T est une affinité de coefficient k si et seulement si la matrice A n'admet pour valeurs propres que 1 et k, et si les espaces propres associés sont supplémentaires (la somme de leurs dimensions est égale à n, l'une d'elle pouvant être nulle).
- En particulier, si k = 0, l'affinité est une projection (la matrice A représente une projection vectorielle dans
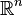
- Si k = − 1, alors l'affinité est une symétrie (la matrice A représente une symétrie vectorielle).
- Si A n'admet qu'une seule valeur propre
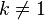
- En particulier, si k = 0, l'affinité est une projection (la matrice A représente une projection vectorielle dans