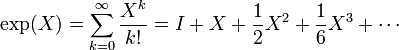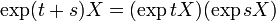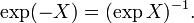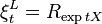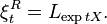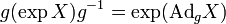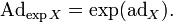Application exponentielle - Définition
La liste des auteurs de cet article est disponible ici.
Théorie de Lie
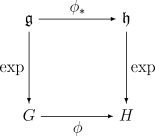
Dans la théorie des groupes de Lie, l'application exponentielle est une application allant de l'algèbre de Lie d'un groupe G vers ce groupe, qui permet de recapturer la structure locale de G à partir de celle de l'algèbre. L'existence de cette application est l'une des principales justifications pour étudier les groupes de Lie à l'aide de leurs algèbres.
La fonction exponentielle ordinaire de l'analyse réelle est un cas particulier d'application exponentielle, en prenant pour G le groupe multiplicatif des réels non nuls (dont l'algèbre de Lie est le groupe additif formé de tous les réels). L'application exponentielle d'un groupe de Lie satisfait de nombreuses propriétés analogues à celle de l'exponentielle usuelle, mais présente aussi avec elle d'importantes différences.
Définitions
Soit G un groupe de Lie et
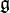
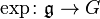
- C'est l'application exponentielle d'une connexion affine canonique invariante à gauche sur G, telle que le transport parallèle soit donné par les translations à gauche.
- C'est aussi l'application exponentielle d'une connexion affine canonique invariante à gauche sur G. Ces deux connections sont en général distincte, mais elles possèdent les mêmes géodésiques (orbites de sous-groupes à un paramètre agissant par la multiplication à gauche ou à droite), donc donnent naissance à la même application exponentielle.
- Elle est donnée par exp(X) = γ(1), où
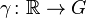
- Si G est un groupe de matrices, alors l'application exponentielle coïncide avec l'exponentielle de matrices, et est donné par le développement en série usuel:
-
-
- (où I est la matrice identité).
- Si G est compact, il a une métrique riemannienne invariante par translations gauche et droite, et l'application exponentielle est ausi l'application exponentielle de cette métrique.
Exemples
- Le cercle unité centré en 0 du plan complexe est un groupe de Lie (appelé le groupe du cercle, et noté T ; c'est le sous-groupe multiplicatif des complexes de module 1) dont l'espace tangent en 1 peut être identifié avec l'axe des imaginaires purs,
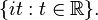
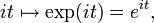
Propriétés
- Pour tous les
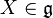
-
-
- L'application exponentielle
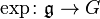
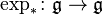
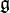
- L'image de l'application exponentielle est toujours contenue dans la composante connexe de l'identité de G. Quand G est compact, l'application exponentielle est surjective sur cette composante. L'image de l'application exponentielle du groupe SL2(R) (connexe mais non compact) n'est pas ce groupe entier.
- L'application γ(t) = exp(tX) est la courbe intégrale passant par l'identité pour les deux champs de vecteurs (invariants à droite et à gauche) associés à X.
- La courbe intégrale passant par

-
- Soit
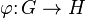
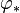
- En particulier, appliqué à l'action adjointe d'un groupe G, nous avons
-