Automate cellulaire - Définition

Théorie des automates cellulaires

Si la popularité du modèle des automates cellulaires vient en grande partie d'une approche expérimentale, il fut dès l'origine abordé comme un objet mathématique par Von Neumann. La plupart des travaux formels sur les automates cellulaires utilisent la définition ci-dessous bien que le modèle admette de nombreuses intéressantes.

Une définition formelle

Un automate cellulaire est un 4-uplet (d,Q,V,δ) où :

• d est la dimension de l'automate, son réseau est alors , l'espace discret de dimension d ;
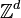
• Q, un ensemble fini, est son alphabet ;
• est son voisinage (un sous-ensemble fini du réseau) ;
• est sa règle locale de transition et a = | V | est l'arité de l'automate.

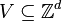
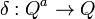
On appelle alors configuration l'attribution d'un état à chaque cellule du réseau : une configuration est un élément de , c'est-à-dire une fonction de dans Q.

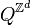
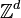
À cette description finie et locale, on associe la fonction globale d'évolution de l'automate, , qui agit sur les configurations et qui est définie par pour toute configuration (où ).

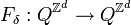
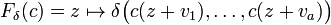
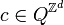
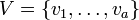
Systèmes dynamiques

Les automates cellulaires ont été étudiés comme des systèmes dynamiques dès les années 1960 avec les travaux de G. A. Hedlund. Lorsque la dimension d et l'alphabet Q sont fixés, on peut munir l'espace des configurations de la métrique de Cantor par la distance d_C définie par

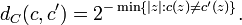
L'ensemble des automates cellulaires d'alphabet Q et de dimension d est alors caractérisé par le théorème de Curtis-Hedlund-Lyondon : F est la fonction globale d'un tel automate cellulaire si et seulement si c'est une fonction continue de qui commute avec les fonctions de décalage (à toute position z dans le réseau de cellules correspond une fonction de décalage ).

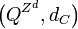
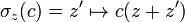
À partir de là, les automates cellulaires peuvent être étudiés avec tout l'outillage de la théorie des systèmes dynamiques classique, de la théorie du chaos et de la théorie ergodique, lorsque l'on munit l'espace des configurations d'une mesure.

Cette branche de la théorie des automates cellulaires reste largement ouverte et fait toujours l'objet de recherches (voir ici pour un exemple de question importante non résolue à ce jour).

Modèle de calcul et constructions algorithmiques

• l'algorithme de P. C. Fischer pour reconnaître les nombres premiers
• le problème de la ligne de fusiliers : une solution ayant 6 états seulement a été publiée par Jacques Mazoyer, il a également prouvé qu'il n'y avait pas de solution à 4 états.

Automates cellulaires universels

On peut considérer les automates cellulaires aussi bien comme des systèmes dynamiques discrets que comme des systèmes de calcul. Ainsi, chaque automate est capable de réaliser certains calculs (plus ou moins intéressants) ou d'exhiber certains comportements dynamiques (plus ou moins complexes). Que l'on adopte l'un ou l'autre des points de vue, on peut se poser une même question : existe-t-il un automate capable de faire tout ce que peuvent faire les automates cellulaires ? Un tel automate est alors dit universel.

La notion d'universalité correspond à une idée très simple et très générale, mais il faut prendre garde au fait que selon le sens que l'on met derrière l'expression "capable de faire" les automates universels ne sont pas les mêmes. On peut distinguer deux types de notions d'universalité pour les automates cellulaires : l'universalité Turing qui est associée à la capacité de calcul et l'universalité intrinsèque qui est associée à la capacité de produire certains comportements dynamiques.

Le fait remarquable est que pour chacune de ces notions il existe des automates universels. Il faut noter également que la notion d'universalité intrinsèque est plus forte que l'universalité Turing : en effet, sans rentrer dans les détails, un automate capable de simuler tous les automates peut en particulier simuler un automate Turing-universel et donc effectuer tous les calculs Turing. En revanche, il existe des automates cellulaires Turing-universels qui ne sont pas intrinsèquement universels.

Universalité Turing

L'universalité Turing est une adaptation aux automates cellulaires de l'universalité pour le calcul. On peut définir cette notion comme la capacité d'un automate à simuler une machine de Turing universelle. Cette possibilité de simulation d'une machine de Turing par un automate cellulaire est très simple et était connue dès les travaux de John von Neumann. Il existe plusieurs manières de la formaliser et ce qui suit est l'une des plus simples. Si M est une machine de Turing fonctionnant avec un alphabet de ruban Σ et un ensemble d'état Q, on peut définir un automate cellulaire A capable de simuler M :

• l'alphabet de A est  : ainsi chaque cellule de A possède un état (σ,q) formé d'une composante σ qui correspond au contenu du ruban et d'une composante q qui correspond à l'absence ( ) ou la présence ( ) d'une tête de Turing à cette position et qui donne le cas échéant son état ;
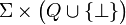
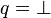
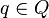
• son voisinage est { − 1,0,1}
• le comportement de A consiste à reproduire les mouvements de la tête de Turing sur la première composante et les modifications du ruban sur la deuxième composante exactement comme le ferait M :

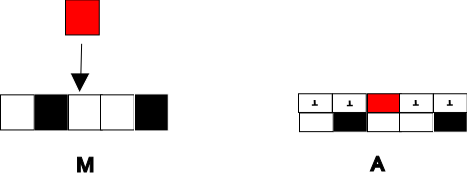
On rencontre souvent une acception plus générale (mais plus informelle) de l'universalité Turing : un automate cellulaire est Turing-universel s'il est capable de simuler un système de calcul Turing-complet. Le terme simuler est rarement formalisé dans un cadre général. Le point important est que la transformation des entrées/sorties du système simulé vers des entrées/sorties du simulateur reste simple : sans cette condition, on obtient une notion dénuée d'intérêt car des automates qui ne font rien (l'identité par exemple) deviennent universels grâce à des transformations d'entrées/sorties qui font tout le calcul à leur place.

Universalité intrinsèque

Un automate cellulaire intrinsèquement universel est un automate capable de simuler pas à pas le comportement de n'importe quel automate cellulaire de même dimension. Plus précisément, l'idée de simulation pas à pas repose sur les principes suivants :

• dans l'automate simulateur, on forme des groupes de cellules voisines, tous identiques, qui recouvrent régulièrement le réseau de cellules ; chaque groupe dans le simulateur représente une cellule simple de l'automate simulé ;
• à chaque état de l'automate simulé correspond une configuration d'états de groupe dans l'automate simulateur ;
• l'automate simulateur peut utiliser plusieurs étapes pour simuler une étape de l'automate simulé.

Ainsi, par exemple, le Jeu de la vie est capable de simuler pas à pas l'automate D à 2 états (noir et rouge) qui effectue un simple décalage des états vers le sud-est :

• les groupes de cellules dans le Jeu de la vie sont des carrés de cellules ;
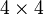
• l'état noir de B correspond à un groupe de cellules toutes mortes et l'état rouge correspond à un planeur entouré de cellules mortes et ajusté dans une certaine position au sein du groupe ;
• une étape de B est simulée toutes les 16 étape du Jeu de la vie.

Ainsi, pour simuler le comportement de B à partir d'une certaine configuration initiale, il suffit de fabriquer une configuration du Jeu de la vie où chaque groupe est soit rempli de cellules mortes, soit d'un planeur selon l'état de la cellule qui lui correspond dans B.

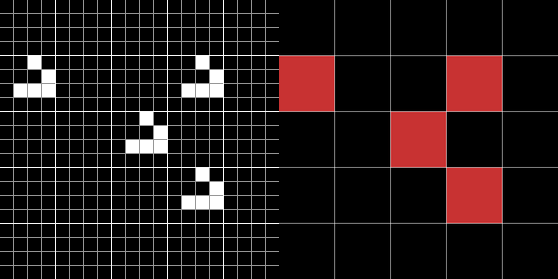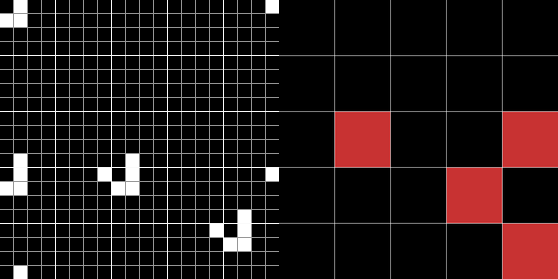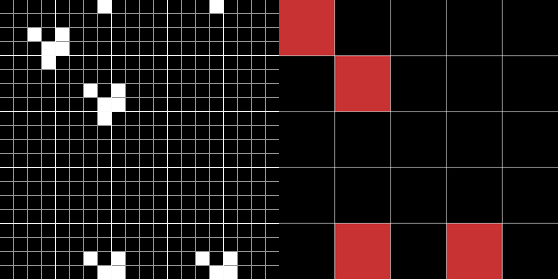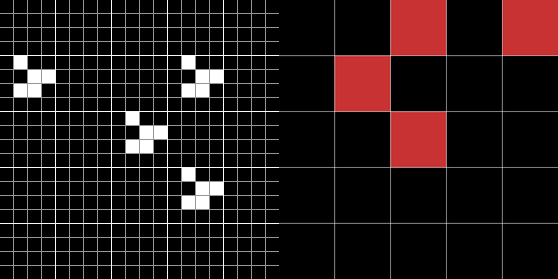
Il est remarquable qu'avec ce principe de simulation très simple certains automates soient capables de simuler n'importe quel automate cellulaire à partir de n'importe quelle configuration : c'est le cas du Jeu de la vie comme expliqué dans la . Bien entendu, pour simuler des automates avec de plus en plus d'états, un automate intrinsèquement universel utilise des groupes de cellules de plus en plus grands. En effet, avec un type de groupe de cellules fixés, il n'existe qu'un nombre fini de simulations possibles. Ainsi, quand on observe une évolution du Jeu de la vie sur un écran (aussi grand soit il), on ne voit pas tous les comportement que le Jeu de la vie est capable de simuler ; pourtant cet automate est capable de produire tous les comportements d'automate cellulaire.

Exemples

Historiquement, le premier automate cellulaire construit ayant une propriété d'universalité (Turing en l'occurrence) est le constructeur universel de John von Neumann : il s'agit d'un automate de dimension 2 à 29 états qui est en outre capable de s'auto-répliquer.

Concernant la notion d'universalité intrinsèque, il faut attendre les années 70 avec les travaux de E. R. Banks qui proposa un automate cellulaire de dimension 2 à 2 états et 5 voisins. Il propose également un automate de dimension 1 intrinsèquement universel avec 5 états mais dont le voisinage est énorme.

L'exemple le plus célèbre d'automate universel est certainement le Jeu de la vie. Il fut prouvé Turing universel dans l'ouvrage Winning Ways for your Mathematical Plays. La preuve consiste à construire des morceaux de configurations qui peuvent être assemblés et qui correspondent à tous les composants nécessaires à la fabrication de circuits logiques (fils, croisements de fils, duplication, portes logiques, etc). On peut trouver une construction complète d'une machine de Turing dans le Jeu de la vie sur le site de Paul Rendell. À partir des mêmes idées, le Jeu de la vie fut plus récemment prouvé intrinsèquement universel.

Pour la dimension 1, une percée concernant l'universalité Turing a eu lieu récemment : M. Cook a prouvé que l'automate cellulaire numéro 110 était Turing-universel. Il a présenté ses idées dès 1998 à la conférence CA98, mais ce résultat n'a été (partiellement) diffusé par écrit qu'en 2002 à travers A New Kind of Science de S. Wolfram. En effet, M. Cook était employé par Wolfram Research pour travailler sur le livre A New Kind of Science et ses travaux ne furent pas publiés dans les actes de CA98 suite à une action en justice fondée sur un accord de non divulgation. La preuve complète du résultat de M. Cook a finalement été publiée dans une revue scientifique en 2004.

En revanche, on ne sait toujours pas aujourd'hui si l'automate 110 est intrinsèquement universel ou pas. Le plus petit automate de dimension 1 avec un voisinage de 3 cellules qui ait été prouvé intrinsèquement universel à ce jour comporte 4 états.

Complexité

De façon générale, il est extrêmement difficile de déterminer le comportement global d'un automate cellulaire en examinant sa règle locale de transition. Ceci se traduit par des résultats d'indécidabilité touchant les propriétés les plus simples. Dans ce domaine on peut citer les travaux de Jarkko Kari qui, en utilisant de façon astucieuse les résultats déjà connus sur les pavages, a montré que les problèmes suivants étaient indécidables :

• savoir si un automate cellulaire est nilpotent (i.e. toutes les configurations mènent au bout d'un temps fini vers une même configuration uniforme),
• savoir si un automate cellulaire de dimension peut atteindre toutes les configurations après une étape (problème de la surjectivité),
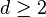
• savoir si un automate cellulaire de dimension est.

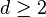
Le fait que des automates cellulaires puissent simuler n'importe quelle machine de Turing amène aussi des problèmes indécidables d'une autre nature. Par exemple, pour certains automates cellulaires, les problèmes suivants sont également indécidables :

• savoir si, étant donné un motif m présent initialement au centre, un motif m' va apparaître au centre au bout d'un certain temps,
• savoir si un motif m peut apparaître arbitrairement tard dans l'évolution ou, au contraire, s'il existe un temps au-delà duquel m n'apparaît plus quelle que soit la configuration de départ.