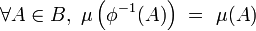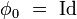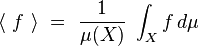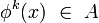Théorie ergodique - Définition

Introduction

La théorie ergodique est une branche des mathématiques née de l'étude de l'hypothèse ergodique formulée par le physicien Ludwig Boltzmann en 1871 pour sa théorie cinétique des gaz. Elle a connu de nombreux développements en relation étroite avec la théorie des systèmes dynamiques et la théorie du chaos.

Notations

Dynamique discrète

L'objet d'étude en théorie ergodique est un triplet ((X,B),μ,Φ) où :

• (X,B) est un espace mesurable, (c’est-à-dire que B est une tribu sur X)

• μ une mesure sur (X,B),

• une application préservant la mesure μ, c’est-à-dire telle que :

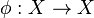
L'application engendre une dynamique discrète : partant d'un point , on obtient successivement x₁ = φ(x₀), puis x₂ = φ(x₁) = φ²(x₀), et ainsi de suite.

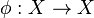
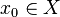
Dynamique continue

On peut étendre l'étude au cas d'une dynamique continue en remplaçant l'application précédente par un flot sur X, c’est-à-dire un groupe continu à un paramètre tel que :

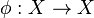
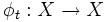
Ce cas est particulièrement important puisqu'il inclut le flot hamiltonien de la mécanique classique, ainsi que le flot géodésique.

Flot ou « cascade » ?

Le cas continu englobe le cas discret, car on peut toujours construire une application discrète à partir d'un flot continu, en posant par exemple φ = φ_{t = 1} pour l'unité de temps. Poursuivant l'analogie avec le vocabulaire de l'hydrodynamique, l'application discrète est alors parfois baptisée « cascade » par certains mathématiciens.

Théorème ergodique de Birkhoff

Moyenne temporelle & moyenne microcanonique

Soit f une « bonne » fonction sur X. On définit sa valeur moyenne temporelle par la limite (si elle existe) :

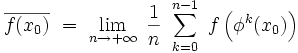
Elle dépend a priori de la condition initiale x₀. On peut également définir la moyenne spatiale de f, ou moyenne microcanonique, par :

La moyenne spatiale et la moyenne temporelle n'ont a priori pas de raison d'être égales.

Théorème de Birkhoff (1931)

Lorsque l'application φ est ergodique, moyenne spatiale et moyenne temporelle sont égales presque partout. Ce résultat constitue le célèbre théorème ergodique de Birkhoff.

Temps de séjour moyen

Soit un sous-ensemble mesurable de X. On appelle temps de séjour dans A le temps total passé par le système dynamique dans A au cours de son évolution. Une conséquence du théorème ergodique est que le temps de séjour moyen est égal au rapport de la mesure de A par la mesure de X :

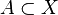
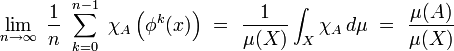
où χ_A est la fonction indicatrice de A.

Récurrences

Théorème de récurrence de Poincaré

• Récurrence d'un point : Soit un sous-ensemble mesurable. Un point est dit récurrent par rapport à A si et seulement s'il existe une infinité d'entiers pour lesquels :

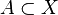
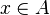
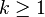
• Théorème de récurrence de Poincaré : Soit un sous-ensemble mesurable de mesure strictement positive. Alors, presque tous les points sont récurrents par rapport à A.

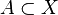
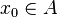
Temps de récurrence moyen

• Un instant k tel que φ^k(x) est dans un ensemble mesurable A est appelé instant d'occurrence de A. Ces instants d'occurrence peuvent être classés par ordre croissant dans un ensemble dénombrable : avec k_{i + 1} > k_i.

• Les différences positives r_i = k_i − k_{i − 1} entre deux instants d'occurrence consécutifs sont appelés les durée de récurrence de A.

Une conséquence du théorème ergodique est que la durée moyenne de récurrence de A est inversement proportionnelle à la mesure de A , sous l'hypothèse que la condition initiale x appartient à A, de telle sorte que k₀ = 0.

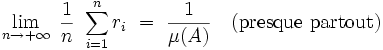
Ainsi, plus l'ensemble A est « petit » et plus il faut attendre longtemps en moyenne avant d'y retourner. Malheureusement, ce résultat ne nous renseigne pas sur l'écart-type de la distribution des temps de récurrence. Par exemple, pour le modèle des urnes d'Ehrenfest, Kac a pu démontrer que cet écart-type tendait vers l'infini lorsque le nombre de boules du modèle tendait vers l'infini, de telle sorte que des fluctuations importantes autour de la durée moyenne de récurrence devenaient de moins en moins improbables.