Autostabilisation - Définition

Variantes de l'autostabilisation

Selon les circonstances et les problèmes posés, l'autostabilisation est parfois considérée comme inutilement contraignante ou, au contraire, insuffisamment forte. C'est là qu'interviennent des variantes, relâchements ou renforcements de la définition de base.

La pseudo-stabilisation

La pseudo-stabilisation, ou pseudo-autostabilisation, est un relâchement des contraintes de l'autostabilisation. Au lieu d'exiger que toute exécution se termine dans ℒ, on exige que toute exécution réalise une tâche abstraite, c'est-à-dire un prédicat sur le système. Par exemple, pour spécifier l'exclusion mutuelle, on peut exiger que tous les processus du système possèdent un privilège donné infiniment souvent, mais que deux processus ne le possèdent jamais en même temps. Ceci ne permet pas de définir les exécutions légitimes, car elles doivent reposer sur l'état du système ; or, dans la définition d'une tâche abstraite, c'est impossible car on ne sait rien de la façon dont les processus sont réalisés. La pseudo-stabilisation est moins forte et moins contraignante que l'autostabilisation, car tout système autostabilisant est pseudo-stabilisant, mais la réciproque est fausse. Burns, Gouda et Miller, qui ont introduit cette notion en 1993, estiment qu'elle est généralement suffisante en pratique.

Première boucle

Perte d'un message

Deuxième boucle

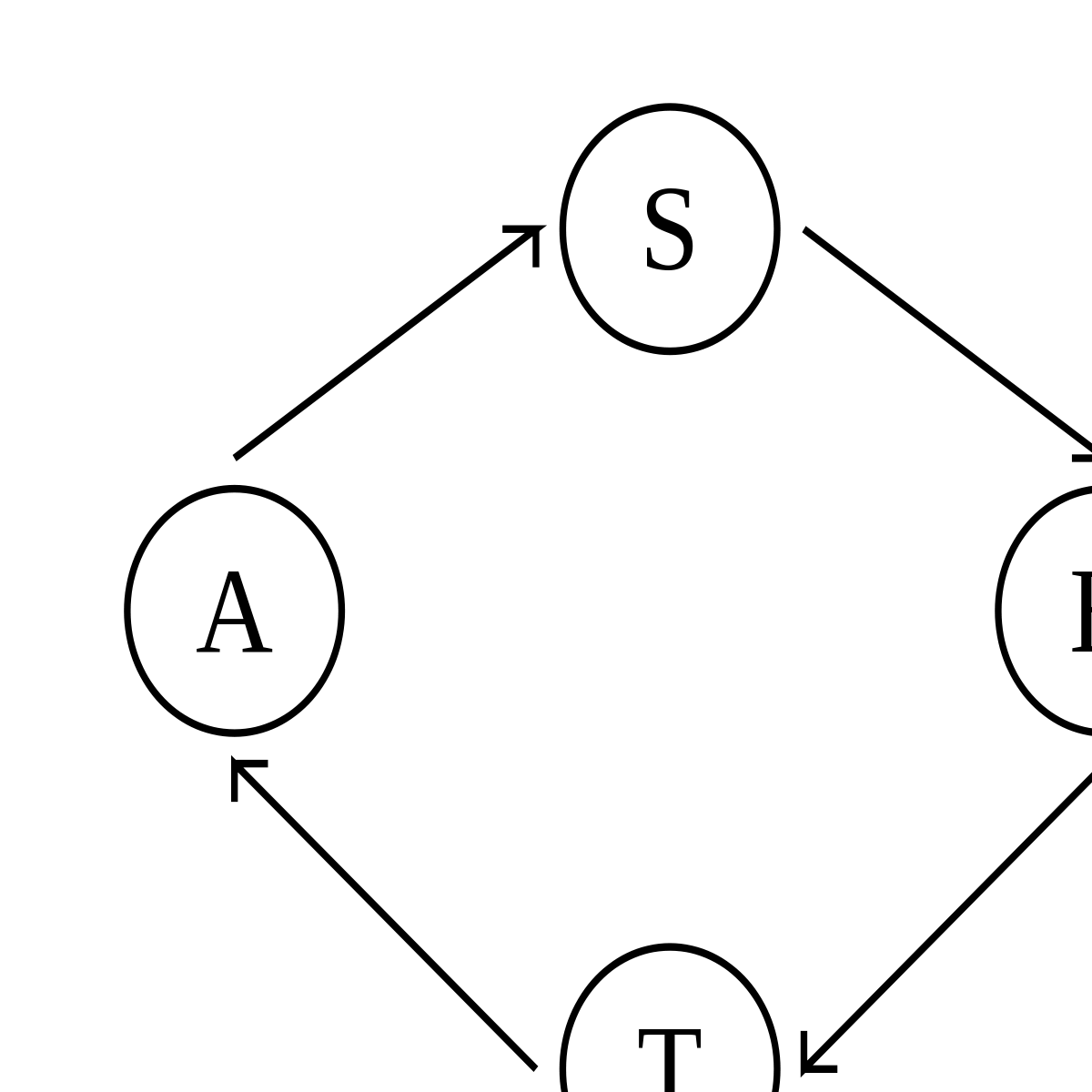
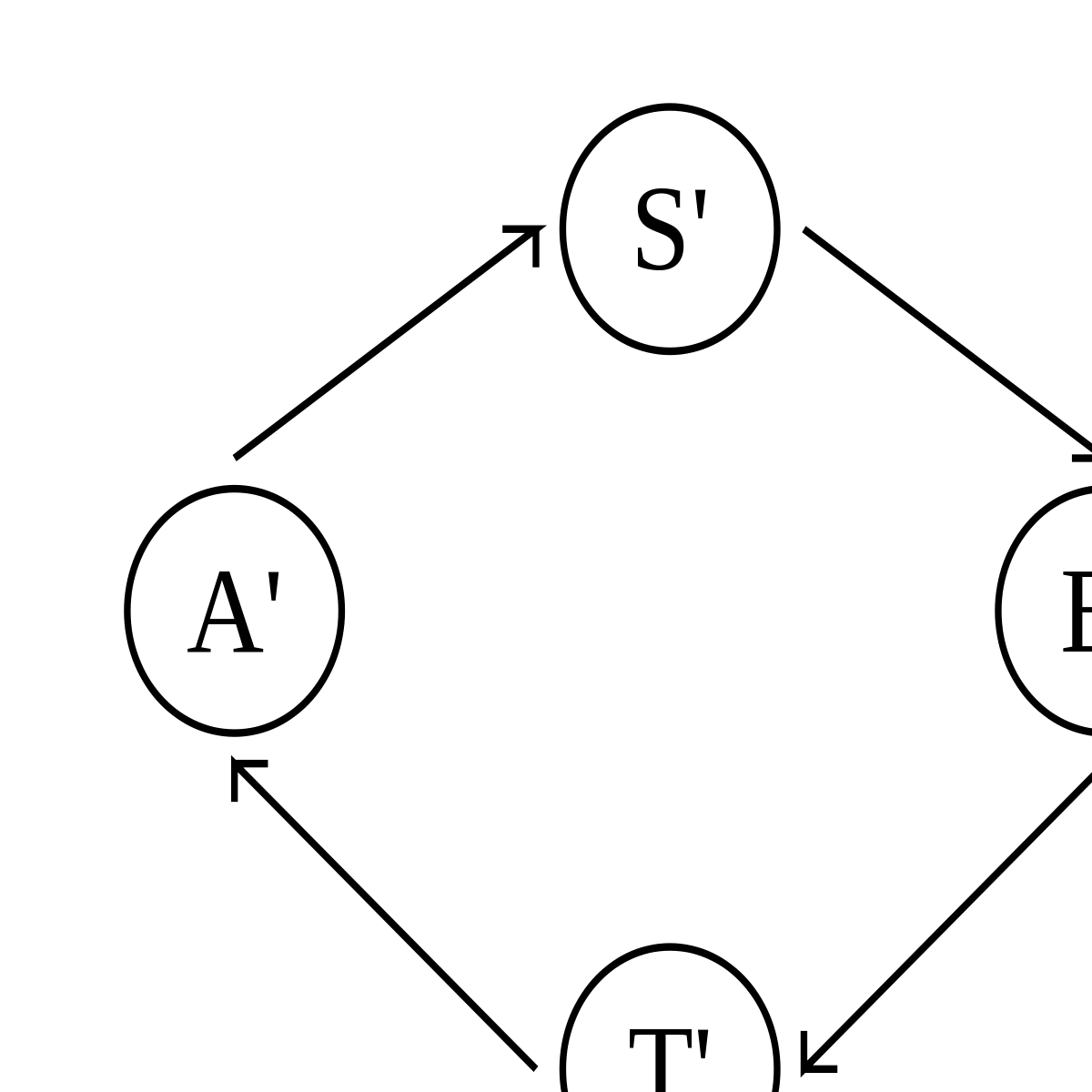
L'exemple classique de pseudo-stabilisation illustré ci-dessus est un système dans lequel deux processus s'échangent des messages. En fonctionnement normal, le système est dans l'état A ; il envoie un message, ce qui fait passer le système dans l'état S ; l'autre processus reçoit le message, ce qui fait passer le système dans l'état B ; le deuxième processus envoie à son tour un message, ce qui fait passer le système dans l'état T ; le premier processus reçoit le message, et le système est de retour dans l'état A. Le problème est que le canal par lequel passent les messages peut perdre un message, auquel cas le système récupère de cette perte en passant dans l'état A'. La définition de A' est totalement dépendante de la méthode utilisée pour récupérer de la perte du message ; elle est donc inconnue au niveau de la tâche abstraite. À partir de A', l'exécution se poursuit de façon similaire : A', S', B', T', A', etc.

Comme la perte d'un message peut se produire, le système n'est pas autostabilisant vers la boucle A, S, B, T. D'un autre côté, cette perte de message peut très bien ne jamais arriver, ce qui fait que le système n'est pas non plus autostabilisant vers la boucle A', S', B', T', ni vers l'ensemble des états possibles. En revanche, ce système, sans être autostabilisant, est bien pseudo-stabilisant pour la tâche abstraite selon laquelle les deux processeurs s'échangent des messages à tour de rôle, puisque la perte d'un message ne remet pas en cause cette définition.

La superstabilisation

L'idée de la superstabilisation, introduite par Shlomi Dolev et Ted Herman, est de considérer le changement de topologie, c'est-à-dire l'ajout ou le retrait d'un lien de communication dans le système, comme un événement spécial dont tout processus concerné est averti et qui déclenche une procédure appelée section d'interruption. Grâce à cela, le système est capable de garantir qu'une propriété de sûreté particulière, le prédicat de passage, reste toujours vérifiée pendant la stabilisation lorsqu'un changement de topologie se produit à partir d'une configuration sûre. Ceci renforce les garanties données par le système face à un type de défaillance très fréquent en pratique. Plusieurs problèmes de base de l'algorithmique répartie ont été résolus par un algorithme superstabilisant, par exemple l'exclusion mutuelle, la construction d'un arbre couvrant et la construction d'un arbre de Steiner.

La stabilisation instantanée

Au lieu de laisser le système appliquer son algorithme et se corriger si nécessaire, il est possible de faire l'inverse : surveiller le système en permanence pour chercher les incohérences et les corriger immédiatement, avant de laisser un pas s'effectuer. Ainsi, le système se comporte toujours conformément à sa spécification : il est autostabilisant en zéro étape. Un système instantanément stabilisant résiste donc parfaitement aux défaillances transitoires, sans qu'un observateur ne s'aperçoive qu'elles se sont produites.

Pour le moment, seuls quelques algorithmes basiques instantanément stabilisants ont été développés, par exemple pour le problème du parcours en profondeur d'un arbre ou la communication point à point dans un réseau commuté. Il est possible de rendre instantanément stabilisant tout algorithme autostabilisant en mémoire partagée, mais la transformation a un coût élevé. Enfin, la stabilisation instantanée est utilisable dans les systèmes à passage de messages, mais là encore, avec un surcoût considérable.

L'approche probabiliste

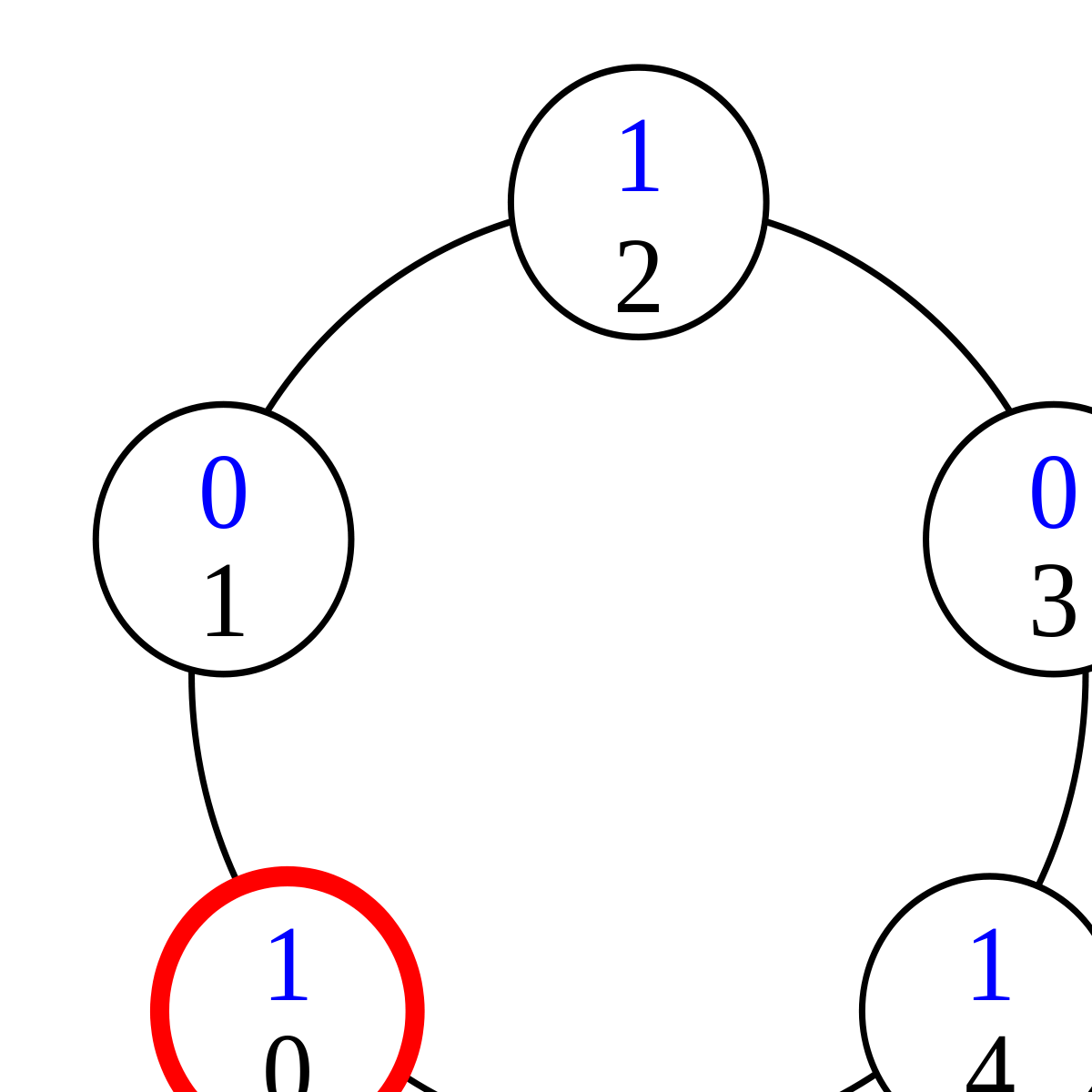
Dans une version étendue de son article fondateur, Dijkstra établit qu'il ne peut pas exister d'algorithme d'anneau à jeton autostabilisant dans lequel tous les processus sont identiques, à moins que la taille de l'anneau ne soit un nombre premier. En 1990, Ted Herman apporte un moyen de surmonter cette limitation : obliger l'ordonnanceur à se comporter non plus de façon non-déterministe, mais de façon probabiliste, avec pour preuve de concept l'algorithme d'anneau à jeton autostabilisant probabiliste suivant : le nombre de processus est impair, et l'état de chaque processus est un bit, qui ne peut donc valoir que 0 ou 1. Un processus possède un jeton si et seulement si son état est le même que celui de son voisin de gauche. Dans la configuration (1) ci-dessous, le processus 0 a un jeton car son état est 1, comme pour le processus 4, et aucun autre processus n'a de jeton. Tout processus qui a un jeton est susceptible d'être choisi par l'ordonnanceur pour changer d'état. Dans ce cas, son nouvel état est tiré au sort : 0 ou 1, avec probabilité ½.

Configuration (1)

Configuration (2)

L'interprétation de cette règle en pratique est que le processus a une chance sur deux de garder son jeton, et une chance sur deux de le passer au processus suivant sur l'anneau. Dans la configuration (1), si le processus qui a le jeton tire l'état 1, rien ne change. S'il tire l'état 0, il n'a plus de jeton, car son nouvel état est identique à celui de son voisin de gauche. En revanche, le processus 1 a maintenant un jeton, car il a le même état que son voisin de gauche.

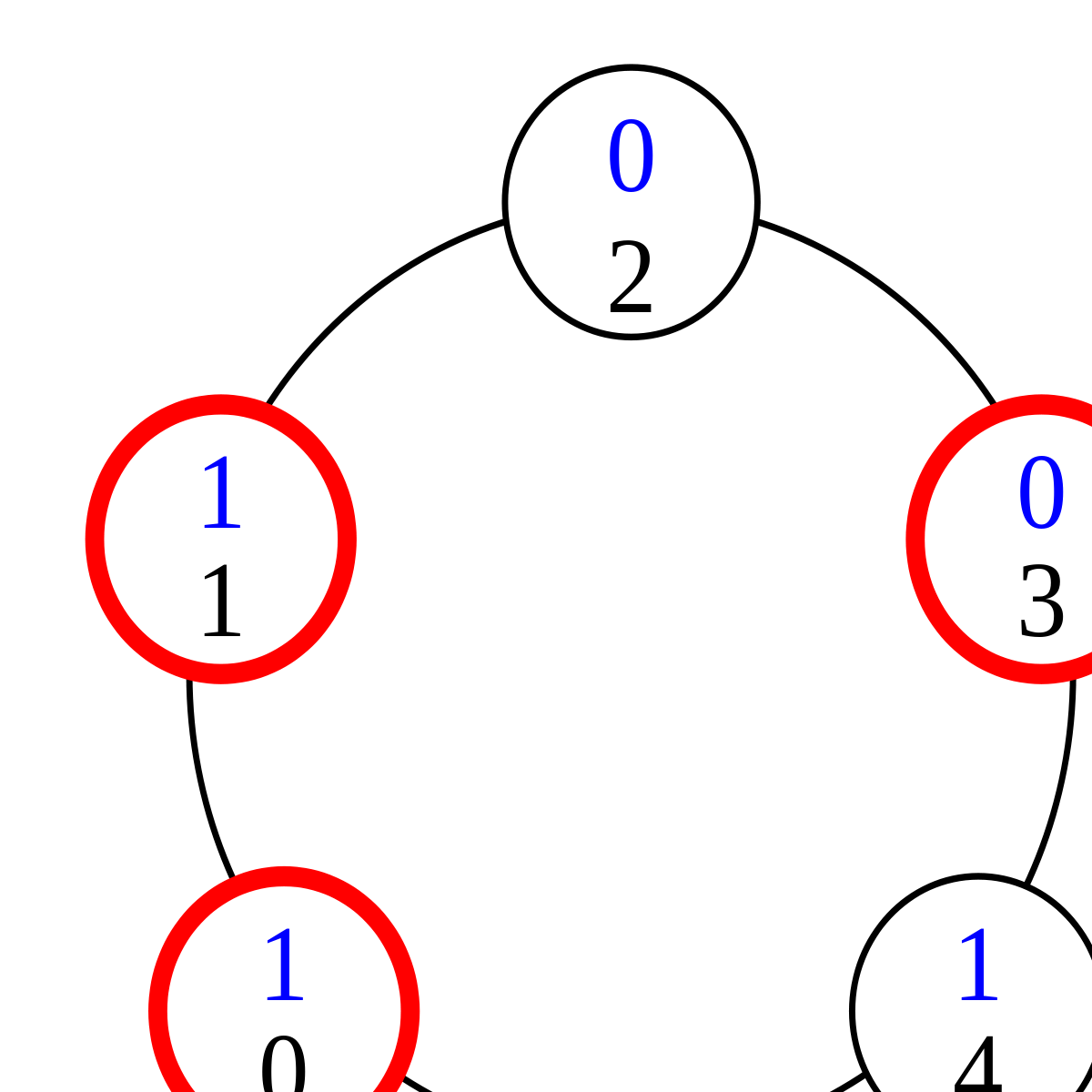
Dans la configuration (2), trois processus ont un jeton. Selon le processus choisi par l'ordonnanceur et le résultat du tirage au sort, après un pas de l'exécution, il peut rester trois jetons ou seulement un. Ainsi, si le processus 1 est choisi, il peut soit garder son jeton, soit le transmettre au processus 2, ce qui ne change pas le nombre de jetons. Mais si le processus 0 est choisi et tire l'état 0, non seulement il perd son jeton, mais le processus 1 perd également le sien. Un ordonnanceur non-déterministe, comme celui utilisé par Dijkstra, pourrait obliger les processus à passer leurs jetons sans jamais les perdre, mais un ordonnanceur probabiliste ne peut pas le faire, car la perte du jeton a une probabilité strictement positive : au cours d'une exécution infinie, elle se produit donc avec probabilité 1.

Dans le cas d'un algorithme probabiliste, il n'est pas possible de calculer un temps de stabilisation, car celui-ci dépend des tirages aléatoires. En revanche, il est possible de calculer son espérance. Initialement, Herman démontre que l'espérance du temps de stabilisation de son algorithme est O(n² log n) étapes. Un calcul plus précis montre par la suite que cette espérance est exactement Θ(n²) étapes. Des recherches plus récentes donnent un cadre général basé sur la théorie des chaînes de Markov pour effectuer ces calculs de complexité dans le modèle probabiliste.