Autostabilisation - Définition

L'anneau à jeton de Dijkstra

Edsger Dijkstra.

Le concept d'autostabilisation est formulé pour la première fois par Dijkstra en 1974 dans un article qui présente trois algorithmes autostabilisants basés sur le concept d'anneau à jeton. Le principe de l'anneau à jeton est de résoudre le problème de l'exclusion mutuelle en faisant circuler un jeton, qui représente le droit pour le seul processus qui le possède d'effectuer une action qui poserait problème si plusieurs processus l'effectuaient en même temps, par exemple envoyer du texte à une imprimante : un processus qui veut imprimer doit d'abord attendre de recevoir le jeton, puis envoyer son texte à l'imprimante ; après quoi, il perd le jeton. Dans le cas d'un anneau à jeton autostabilisant, si le système est perturbé par l'introduction d'un ou plusieurs jetons supplémentaires, il récupère de lui-même de cette défaillance en supprimant tous les jetons présents sur l'anneau, sauf un ; puis il poursuit son exécution en passant l'unique jeton restant comme s'il n'y en avait jamais eu d'autre.

Les n processus (avec n impair), numérotés de 0 à n-1, sont reliés en anneau, c'est-à-dire que le processus i a comme voisin de droite i+1 modulo (n-1) et comme voisin de gauche i-1 modulo (n-1). Autrement dit, le voisin de gauche du processus 0 est le processus n-1 et le voisin de droite du processus n-1 est le processus 0. Chaque processus a un état entier compris entre 0 et 2. On note É l'état d'un processus, D l'état de son voisin de droite et G celui de son voisin de gauche.

L'algorithme présenté ci-dessous est le troisième de l'article, que Dijkstra considère comme le plus abouti. Une exécution sans défaillance est donnée pour montrer comment se comporte normalement le système, puis le problème de la suppression des privilèges surnuméraires est abordé.

Fonctionnement avec un unique privilège

Configuration initiale (1) : seul le processus 0, en rouge, a un privilège.

À chaque pas de l'exécution, un processus est choisi arbitrairement par un ordonnanceur. En pratique, cet ordonnanceur dépend du matériel, du système d'exploitation et de l'environnement dans lequel il fonctionne ; son comportement est donc imprévisible. Le côté arbitraire de ce choix est à la base de la motivation initiale de Dijkstra, qui cherche à savoir si un système peut se comporter correctement en dépit d'un contrôle réparti. Dans cet algorithme, seuls les processus qui ont un privilège peuvent réagir lorsqu'ils sont choisis, en changeant d'état. Les privilèges et les changements d'état associés sont définis par les règles suivantes :

1. Pour le processus 0 : si (É+1) mod 3 = D alors É ← (É-1) mod 3
2. Pour le processus n-1 : si G=D et (G+1) mod 3 ≠ É alors É ← (G+1) mod 3
3. Pour tous les autres processus :
   • si (É+1) mod 3 = G alors É ← G
   • si (É+1) mod 3 = D alors É ← D

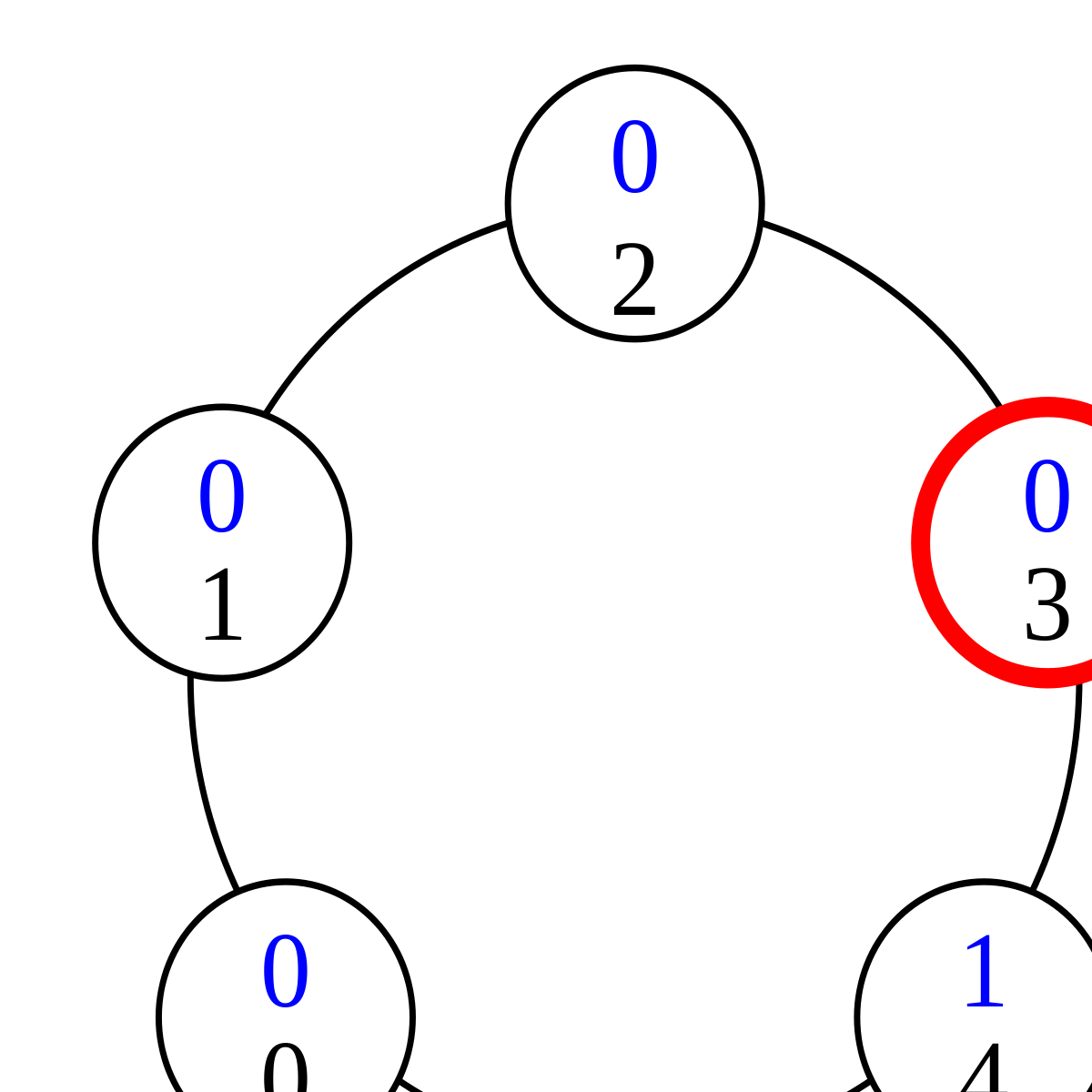
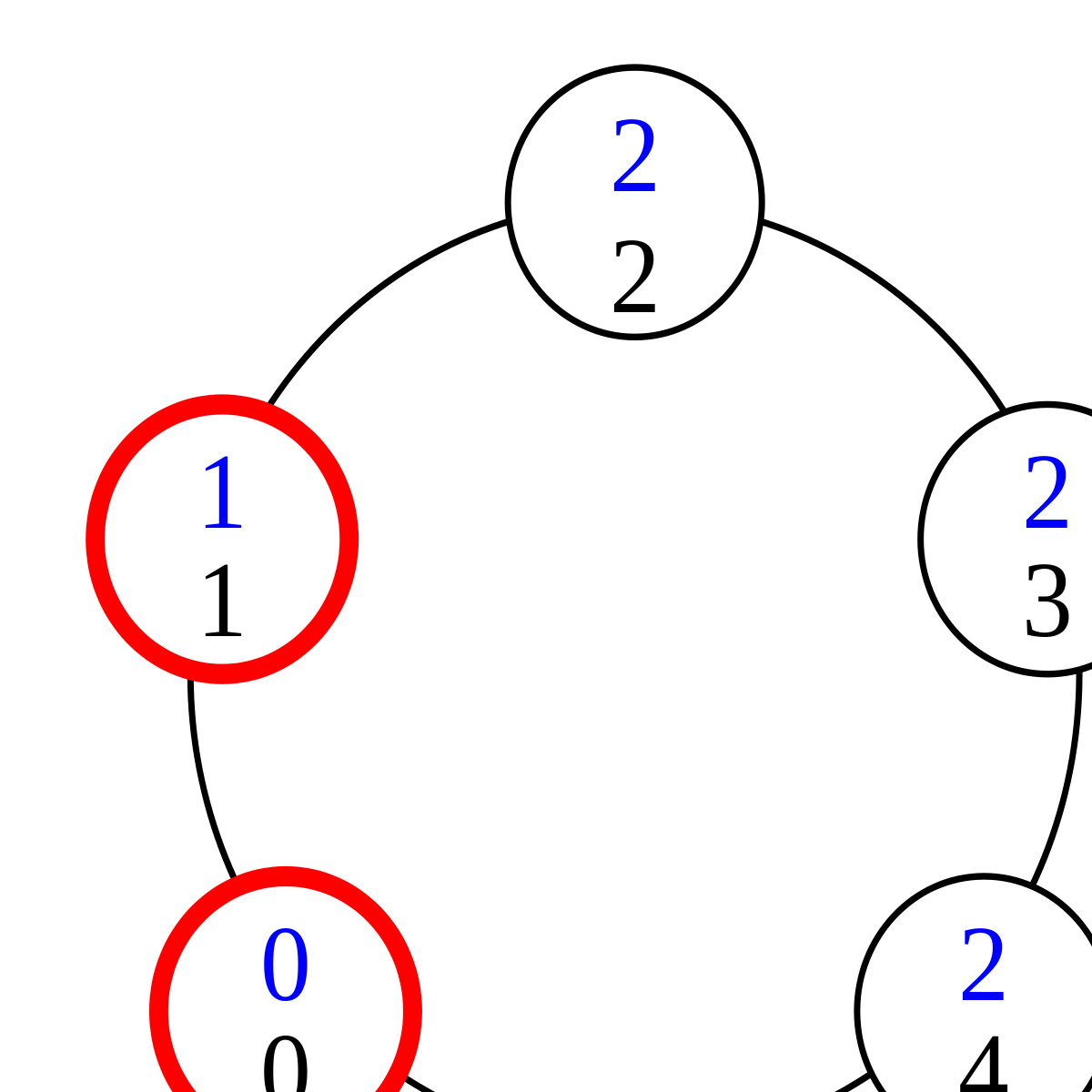
Ici, le privilège représente le fait pour un processus de posséder un jeton. Pour comprendre comment fonctionne cet algorithme lorsqu'il existe un unique privilège, considérons le cas ci-contre. Les numéros de processus sont en noir, les états en bleu. Le processus 0 a un privilège, matérialisé en rouge, en application de la règle 1. En effet, son état est 1 ; en ajoutant 1, on obtient 2, ce qui est l'état de son voisin de droite. En revanche, aucun autre processus n'a de privilège : le processus 4 parce que les états de ses voisins ne sont pas égaux, les autres processus parce qu'aucun processus n'a l'état (2+1) mod 3 = 0.

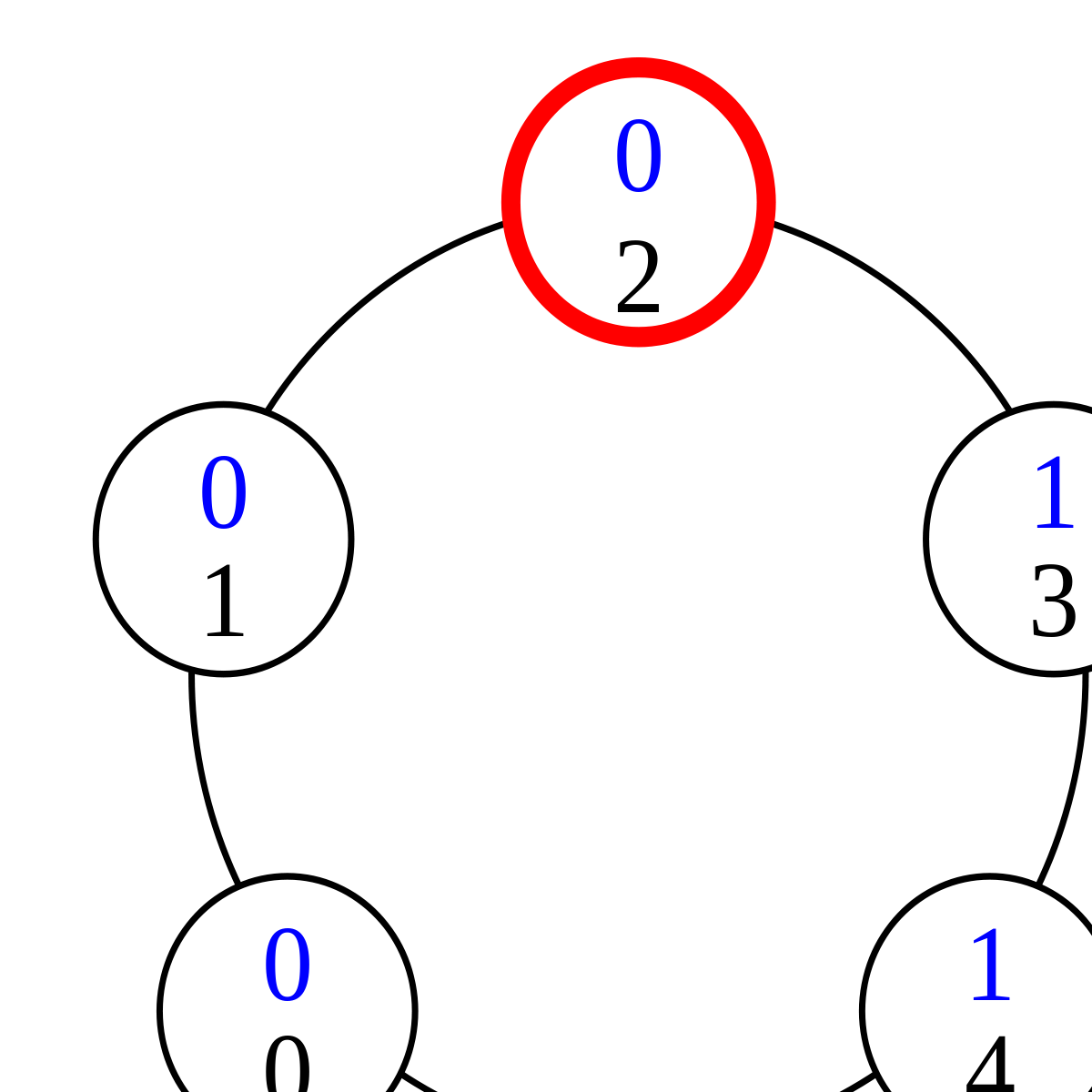
Lors du premier pas de l'exécution, c'est donc le processus 0 qui change d'état. En application de la règle 1, il prend l'état 1-1 = 0. Ceci donne un privilège au processus 1, qui change donc d'état lors du pas suivant de l'exécution. Celle-ci continue ainsi :

Configuration (2)

Configuration (3)

Configuration (4)

Configuration (5)

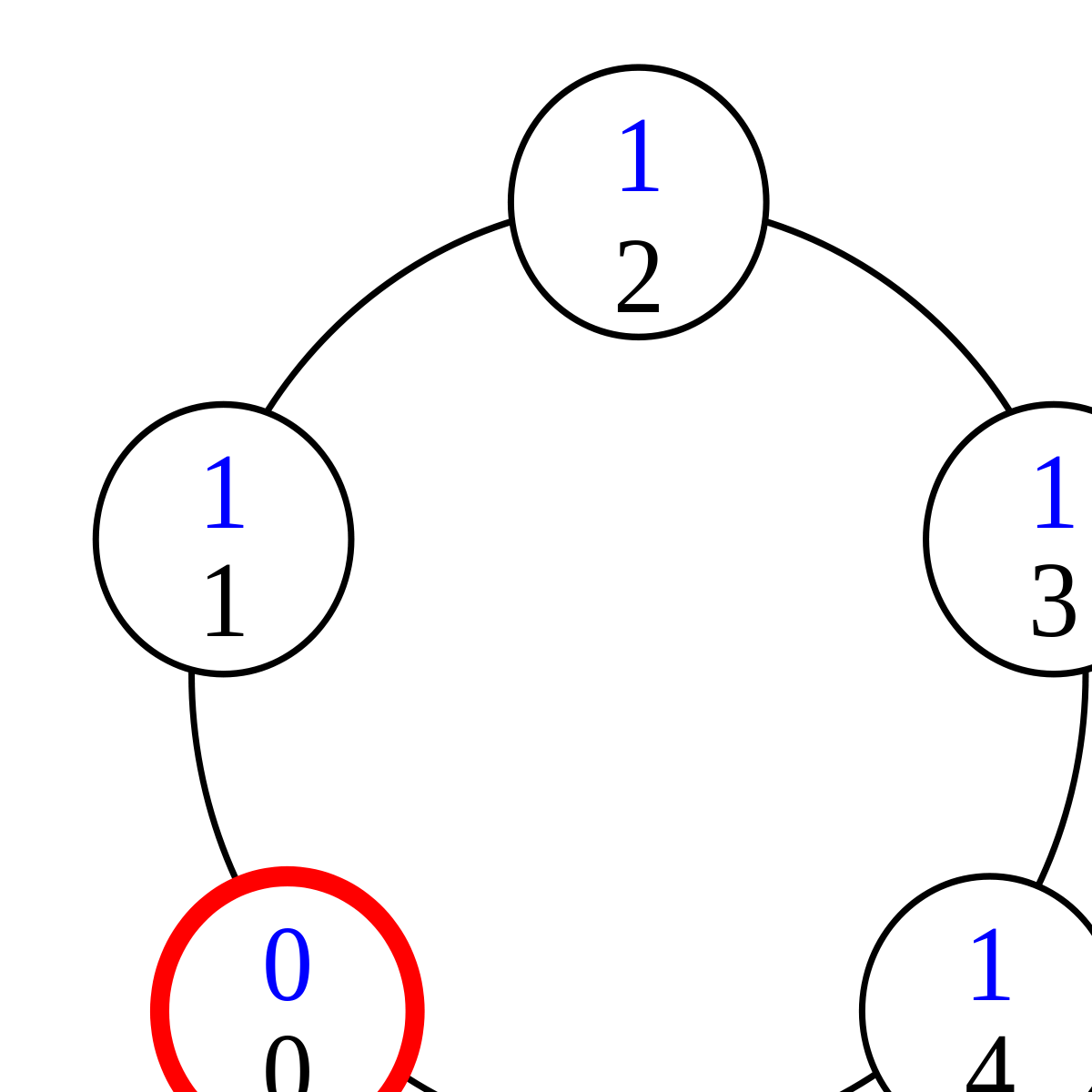
Dans la configuration (5), le processus 4 a le privilège. Il change donc d'état en application de la règle 2, prenant l'état 0+1=1. Ceci donne le privilège au processus 3.

Configuration (6)

Configuration (7)

Configuration (8)

Configuration (9)

Le privilège a été passé, de proche en proche, à tous les processus. La configuration (9) est équivalente à la configuration (1) ; le système est donc prêt à recommencer à passer le privilège selon le même principe. Le constat que « tout se passe bien » montre, informellement, que cette exécution est légitime.

Fonctionnement avec plusieurs privilèges

Pour comprendre comment l'algorithme garantit que le nombre de privilèges atteint forcément 1, il faut d'abord remarquer que les règles ne permettent aucune situation où il n'existerait pas de privilège. En effet, en vertu de la règle 3, dans une telle configuration, les processus dont les numéros vont de 1 à n-2 doivent tous avoir le même état e ; de plus, les processus 0 et n-1 doivent avoir soit l'état e, soit l'état (e-1) mod 3. Or, si le processus 0 a l'état (e-1) mod 3, alors il a un privilège ; s'il a l'état (e-1) mod 3, le processus n-1 a un privilège.

La preuve de correction de cet algorithme, publiée en 1986, s'appuie sur le fait que si plusieurs privilèges existent, alors leur nombre doit nécessairement diminuer. Pour cela, Dijkstra démontre qu'entre deux changements d'état du processus n-1, il se produit forcément un changement d'état du processus 0. Il prouve ensuite qu'il n'existe pas de séquence de pas infinie dans laquelle le processus 0 ne change pas d'état. Enfin, il établit la liste des scénarios possibles pour le comportement du privilège situé le plus à gauche sur l'anneau et démontre que ce privilège disparaît. Par récurrence, après un certain nombre de pas, il ne reste finalement qu'un seul privilège.

Premier cas de collision

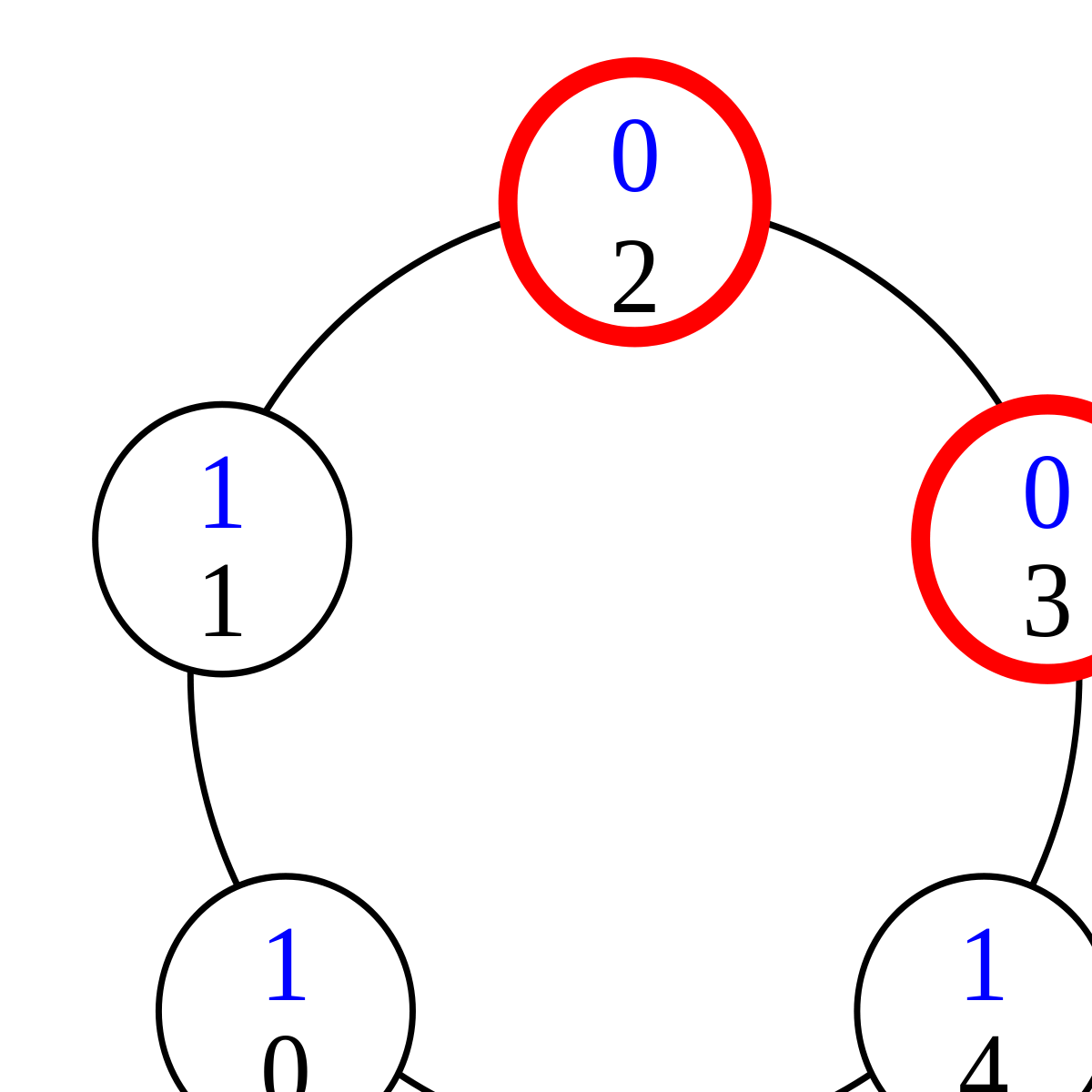
Deuxième cas de collision

Pour voir comment les privilèges surnuméraires disparaissent, il suffit de constater, dans l'exécution normale ci-dessus, que les privilèges circulent de la gauche vers la droite à partir du processus 0 et de la droite vers la gauche à partir du processus n-1. En conséquence, s'il y a deux privilèges sur l'anneau, ils finissent par se rencontrer. Cette situation est illustrée ci-dessus par le premier cas de collision, où ni le processus 0, ni le processus n-1 n'est impliqué. Dans ce cas, dès que l'un des processus privilégiés change d'état, il perd son privilège alors que l'autre processus garde le sien : le nombre de privilèges a diminué de 1.

Le cas de la collision des processus 0 et 1 est particulier (deuxième cas de collision ci-dessus). En effet, si 1 change d'état, son privilège change simplement de « sens », allant désormais de la gauche vers la droite. Cependant, il peut franchir le processus n-1 et doit donc disparaître. Si c'est le processus 0 qui change d'état, de façon analogue, son privilège passe au processus n-1.

Dijkstra n'aborde pas la question du temps de stabilisation de son algorithme, ni dans son article original de 1974, ni dans l'article de 1986 dans lequel il donne la preuve de correction. En 2007, une équipe sans lien avec Dijkstra démontre que cet algorithme se stabilise en O(n²) étapes.

Un nouvel élan

Leslie Lamport.

Bien que l'algorithme présenté ci-dessus ait été utilisé en production, l'article de Dijkstra passe pratiquement inaperçu jusqu'à ce que Leslie Lamport, invité en 1984 à donner une présentation à la conférence PODC, le mentionne comme particulièrement digne d'intérêt. L'autostabilisation devient alors un sujet à part entière en algorithmique répartie, ce que Lamport considère comme une de ses contributions les plus importantes à l'informatique. Des étudiants soutiennent des thèses de doctorat sur l'autostabilisation et se spécialisent dans la recherche sur ce sujet. L'autostabilisation est enseignée à l'université dans le cadre de cours sur l'algorithmique répartie.

En 2000 sort , un livre écrit par Shlomi Dolev, le premier entièrement consacré à l'autostabilisation. Par la suite, plusieurs manuels d'algorithmique répartie et de programmation consacrent un chapitre à ce sujet. Dijkstra reçoit le prix PoDC de l'article influent pour son article de 1974 en 2002, peu avant sa mort. Dès l'année suivante, ce prix est renommé prix Dijkstra en sa mémoire.

Une rencontre internationale sur le thème de l'autostabilisation est lancée en 1989 sous le nom de WSS, Workshop on Self-Stabilizing Systems (« Atelier sur les systèmes autostabilisants »). En 2003, après cinq éditions de l'atelier, la rencontre devient une conférence internationale renommée SSS, Symposium on Self-Stabilizing Systems. En 2005, la conférence élargit son sujet et devient Symposium on Stabilization, Safety, and Security of Distributed Systems (« Congrès sur la stabilisation, la sûreté et la sécurité des systèmes répartis »). Depuis l'édition de 2003, les actes sont .