Autostabilisation - Définition

Définitions

L'autostabilisation est définie dans le formalisme de l'algorithmique répartie, dont elle est une branche. Les définitions ci-dessous se limitent à ce qui est nécessaire pour caractériser l'autostabilisation.

Modèle

Un système est un ensemble de n processus. Chaque processus possède des variables dans lesquelles sont enregistrées les informations que possède le processus. La collection des variables d'un processus est son état.

Deux modèles existent pour représenter les communications entre processus. Le premier modèle est à passage de messages : les processus peuvent communiquer en s'envoyant des messages via des canaux FIFO. Dans ce cas, l'existence ou non d'un canal entre deux processus donnés est définie par la topologie du réseau. L'état d'un canal est défini comme la séquence des messages qu'il contient. Le deuxième modèle est à mémoire partagée. Dans ce cas, il existe un certain nombre de registres partagés et il faut définir quels processus peuvent lire et écrire dans quels registres. L'état d'un registre est la valeur qu'il contient. La configuration du système est la collection de l'état de tous les processus et moyens de communication.

Principe de l'autostabilisation : le système, initialisé dans une configuration quelconque, finit par atteindre une configuration sûre. Toutes les configurations par lesquelles il passe ensuite sont sûres.

Un pas c→c' du système est défini comme l'exécution d'une transition par un processus telle que le système est au départ dans la configuration c, puis, en exécutant une action, passe dans la configuration c'. Au cours d'une transition, un processus peut recevoir un message (resp. lire un registre partagé dans le cas d'un modèle à mémoire partagée), changer d'état, et envoyer des messages (resp. écrire dans des registres partagés).

Une exécution est une suite alternée infinie de configurations et de pas : E = (c₀,a₁,c₁,a₂,c₂,…) telle que pour tout i > 0, l'action a_i fait passer le système de la configuration c_i-1 à la configuration c_i. Elle est dite équitable si elle ne contient pas de séquence infinie de pas au cours de laquelle une certaine transition pourrait être exécutée, mais ne l'est jamais. En d'autres termes, dans une exécution équitable, aucun processus n'est privé de la possibilité d'effectuer une certaine transition.

Autostabilisation

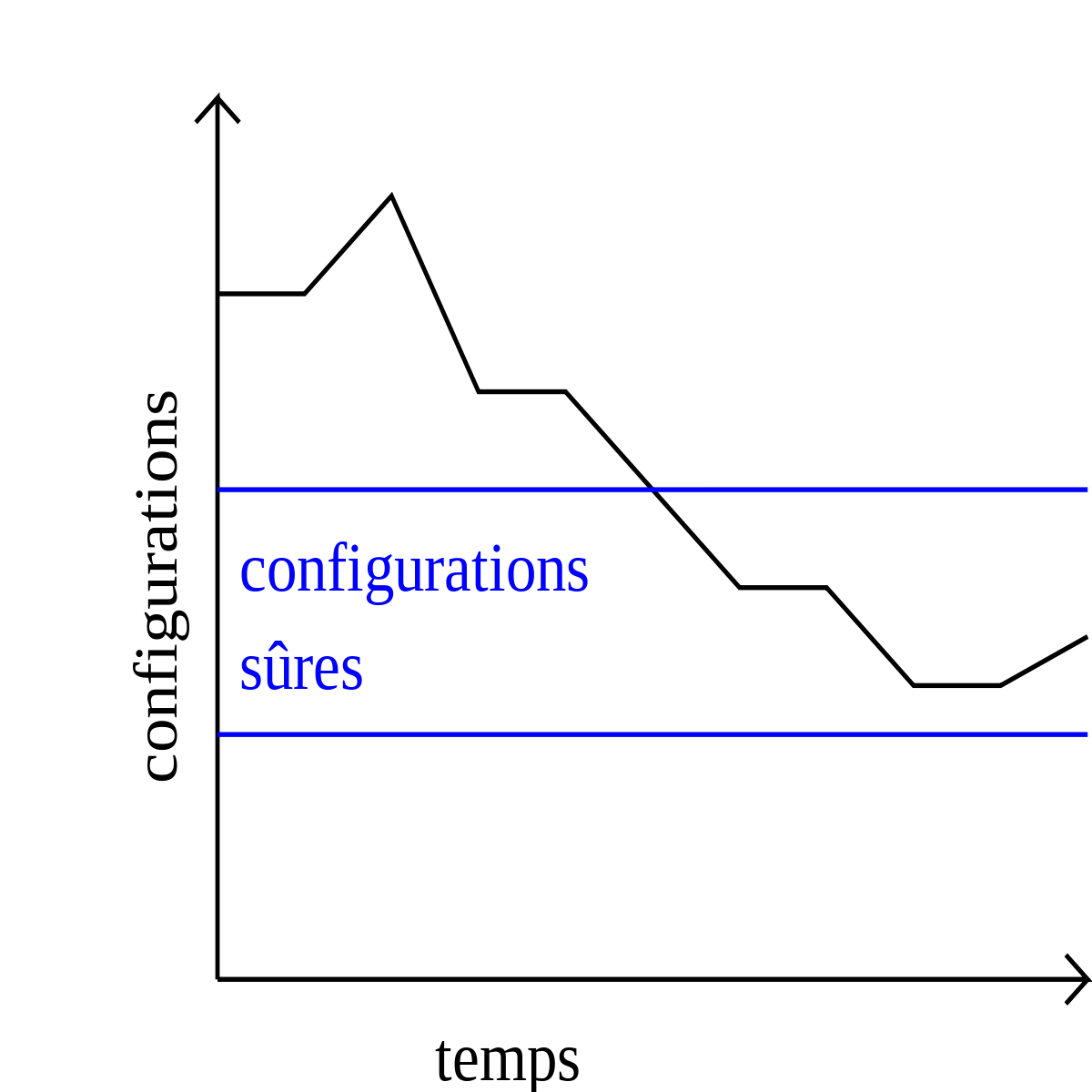
Pour tout système autostabilisant, on définit un ensemble ℒ d'exécutions légitimes. Cet ensemble représente les exécutions dans lesquelles le système se comporte toujours correctement. Une configuration c est dite sûre vis-à-vis de ℒ si et seulement si toute exécution commençant par c est dans ℒ. Un système est autostabilisant vers ℒ si et seulement si toute exécution de ce système, quelle que soit la configuration de départ, atteint une configuration sûre vis-à-vis de ℒ.

Propriété fondamentale

Un système est autostabilisant si et seulement si on peut associer à toute configuration une valeur prise dans un anneau noethérien tel que tout pas de l'exécution commençant dans une configuration non sûre de valeur v fait passer le système dans une configuration de valeur v'

Mesures de complexité

La mesure de l'efficacité d'un algorithme est l'objet de la théorie de la complexité. Elle définit des méthodes permettant de calculer les performances d'un algorithme, principalement selon deux axes : le temps de calcul et la quantité de mémoire utilisée. Dans le cas de l'autostabilisation, on définit le temps de stabilisation comme le temps le plus élevé que le système peut mettre à atteindre une configuration sûre. Dans un système asynchrone, qui ne dispose pas de notion de temps, on définit une ronde comme la plus courte séquence de pas de l'exécution au cours de laquelle chaque processus est activé au moins une fois, ce qui donne une unité dans laquelle on peut exprimer un temps de stabilisation. Les autres mesures de complexité définies dans les systèmes répartis s'appliquent aussi en autostabilisation : on peut ainsi chercher à échanger le moins possible de messages ou à utiliser un minimum de mémoire sur chaque processus.

Interprétation en pratique

À la suite de tout incident qui change l'état du système, l'autostabilisation assure de retrouver automatiquement, après un certain temps de fonctionnement sans nouvel incident, une exécution légitime, et donc un fonctionnement correct. En particulier, cela permet de tolérer toute défaillance transitoire, modification arbitraire de l'état d'un processus au cours d'une exécution. Une telle défaillance peut être causée, par exemple, par un rayon cosmique frappant un circuit intégré. Elle peut aussi être due au fonctionnement du système dans de mauvaises conditions, en particulier en cas de surchauffe ou de surcadencement. Une défaillance transitoire laisse le système dans une configuration quelconque, totalement imprévisible. Ce retour automatique à la normale est particulièrement souhaitable dans un système sur lequel il n'est pas possible de faire intervenir un technicien, par exemple un satellite.

Dans la plupart des systèmes informatiques, le programme lui-même est une donnée enregistrée en mémoire vive. En conséquence, il est sujet aux défaillances transitoires, ce qui empêche l'autostabilisation. La solution est d'enregistrer le programme en mémoire morte. Si le programme doit être chargé en mémoire vive, un chien de garde peut le recharger à partir de la ROM en cas de besoin. Une autre possibilité est de réaliser directement le programme sous forme de circuit intégré.