Calcul de l'effet Sagnac en relativité restreinte - Définition

Calcul du Time Gap

Il est intéressant de dériver le Time Gap d'une autre manière, à la fois plus intuitive et plus simple. Bien qu'elle soit moins rigoureuse (la seule méthode vraiment rigoureuse est celle présentée plus haut).

L'idée est de s'inspirer du décalage constaté lorsque l'on essaie de synchroniser les horloges sur le disque.

On utilise une série d'observateurs et leurs repères inertiels locaux R1, R2, R3, etc. séparés l'un de l'autre de la distance infinitésimale que nous notons dx = Rdθ (où dθ est l'angle infinitésimal qui sépare deux petits domaines successifs).

R est comme d'habitude le repère inertiel.

Chaque observateur est encadré par une paire d'événements : R1 par A et B, R2 par B et C, etc. Les événements sont également séparés (dans R) par la distance dx. Et la vitesse (longitudinale par rapport à dx) est V = Rω comme d'habitude.

Nous considérons dans R que tous les événements sont simultanés de manière à synchroniser les horloges dans R.

Dans R1, à cause de la relativité de simultanéité, A et B seront décalés.

Si R' était inertiel, il y aurait un décalage uniforme et proportionnel à la distance (voir les transformations de Lorentz), C serait un peu plus décalé que B par rapport à A, D, encore un peu plus, et en faisant un tour complet on aurait un décalage croissant puis décroissant (la coordonnée horizontale de R' dans la figure ci-dessus serait croissante en allant vers la droite de la figure puis décroissante en revenant vers la gauche, en dépassant la position d'origine, puis à nouveau croissante en revenant vers la droite) et un décalage final nul entre A et A !, comme il se doit si la synchronisation ne posait pas de problème. La synchronisation pourrait se faire sur le disque.

Mais sur le disque la synchronisation globale n'est pas possible. Chaque observateur va constater un léger décalage entre les événements qui l'encadre et en un tour complet on obtient un décalage total non nul, c'est le Time Gap autour du disque.

Les transformations de Lorentz donnent le décalage de A et B pour R1 :

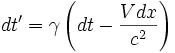
Puisque A et B sont simultanés dans R, on a dt = 0. Donc,

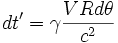
En intégrant sur un tour complet (θ varie de 0 à 2π), on a le Time Gap

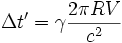
Soit, en utilisant la vitesse réduite B = V / c,

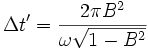
Si l'on emploie la lumière (dans le vide), la vitesse des signaux est c, la différence de longueur parcourue par les deux signaux est donc

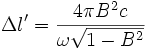
Qu'on peut qualifier de "Length Gap".

Si on envoie un signal de chaque côté, l'un va subir le Time Gap et l'autre le même Time Gap avec le signe opposé. L'écart de temps entre la réception des signaux sera le double, et on retrouve la formule que nous avons calculée.

En utilisant la vitesse des signaux, on peut aussi calculer la longueur qu'ils parcourent pour O' lorsqu'ils font un tour.

On peut qualifier la différence longueur de "Length Gap". C'est la différence de longueur selon qu'on fait le tour dans un sens ou l'autre. Notez que cela montre bien que la géométrie n'est pas euclidienne dans le repère R'. Pire encore, même avec des géométries courbes habituelles (par exemple la surface de la sphère) que vous fassiez le tour d'un cercle dans un sens ou dans l'autre, cela donne la même longueur. Le découpage en "tranche spatiale" comme suggéré dans l'effet Sagnac avant risque donc non seulement de nous donner un espace courbe mais en plus risque de nous poser des difficultés !

Ce length gap n'est pas « universel », car il dépend de la vitesse du signal. En particulier, si un observateur O' placé sur le disque envoie un « arpenteur » mesurer la longueur de la circonférence à faible vitesse (par rapport à la vitesse de rotation et à c), selon le sens il mesurera une longueur différente mais avec une différence extrêmement faible.

Le Length Gap calculé ci-dessus est la différence de longueur "maximale".

Un petit exemple numérique donnera une idée. Soit R = 1 mètre et ω = 100000 (cela fait 16000 tours par seconde, soit presque un million de tours par minute, ce qui est déjà beaucoup, cent fois plus rapide que les moteurs gonflés de la formule 1, et même irréalisable avec des disques réels qui se briseraient sous l'action de la force centrifuge). Supposons que notre arpenteur se déplace à 1 mètre par seconde (sur le disque en rotation).

Alors l'effet Sagnac sera de un centième de milliardième de seconde ! C'est faible mais parfaitement mesurable avec des interféromètres ou même avec des horloges atomiques. Le Length Gap maximal sera de 4 millimètres. Ce qui est mesurable, en particulier par interférométrie. Mais l'arpenteur ne mesurera un Length Gap que d'un centième de nanomètre (plus petit que la taille d'un atome) ! Inutile de faire l'expérience, c'est impossible à mesurer. Même si l'arpenteur, doté d'une horloge, constatera le même Time Gap. Petites causes, grands effets, grandes causes, petits effets !