Calcul de l'effet Sagnac en relativité restreinte - Définition

Quelques remarques sur la détection par interférométrie de l'effet Sagnac

Remarque 1

Le Time Gap que nous venons de calculer s'applique aussi aux composantes de Fourier (la décomposition en différentes fréquences) d'un paquet d'onde associé à deux faisceaux de matière (en mécanique quantique, les particules sont aussi des ondes) se propageant dans les deux directions le long de la circonférence avec la même vitesse.

Bien sûr, seuls les flux de matière sont des entités physiques, tandis que les composantes de Fourier sont juste des entités mathématiques qui ne transportent pas d'énergie. Du point de vue de la détection par interférométrie de l'effet Sagnac, le point crucial est le suivant. En dépit de l'absence d'une signification physique directe et du transfert d'énergie, la vitesse de phase de ces composantes de Fourier obéit à la loi de Lorentz de composition des vitesses et est partagée par les composantes de Fourier dans les deux sens.

De plus, la détection par interférométrie de l'effet Sagnac nécessite que le paquet d'onde associé au faisceau de matière soit suffisamment concentré dans l'espace des fréquences pour permettre l'apparition, dans la région d'interférométrie, d'un réseau de franges observables. Il peut être utile de rappeler que :

• Le déplacement des franges d'interférence Δz dépend de la vitesse de phase de la composante de Fourier du paquet d'onde.
• Dans un repère inertiel synchronisé avec la méthode d'Einstein, la vitesse de toute composante de Fourier d'un paquet d'onde associé à un faisceau de matière, se déplaçant avec la vitesse (en valeur absolue) ou , est donnée par l'expression de de Broglie v_f = v² / c (mécanique quantique).

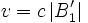
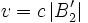
Par conséquent, le décalage des franges dans l'effet Sagnac dû à la différence de temps relativiste calculée ci-dessus est :

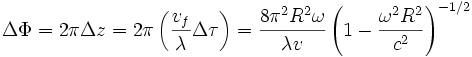
Remarque 2

Notez que Anderson, Stedman et Bilger ont trouvé à l'approximation au premier ordre la différence de temps suivante :

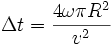
et le déplacement des franges suivant :

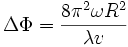
où v est la vitesse "non entraînée" des faisceaux (vitesse dans R).

Bien sûr, cette différence de temps n'est pas en accord avec l'approximation au premier ordre (par rapport à B = ωR / c) de la valeur que nous avons calculée. Cependant, elle est consistante avec l'approximation au premier ordre de la différence de temps générale (avec des vitesses non nécessairement isotropes) pourvu que  : cela représente une situation physique complètement différente où les deux faisceaux sont injectés le long de la circonférence dans des directions opposées avec des vitesses identiques dans le repère inertiel R. La vitesse étant inférieure à c, elle n'est pas invariante et les signaux n'auront pas une vitesse isotrope dans R1.

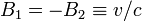
D'un autre côté, la différence de phase qu'ils donnent et qui est la seule quantité observable dans un dispositif d'interférométrie, n'est pas en accord avec la situation physique considérée par ces auteurs. Mais étonnamment, elle est parfaitement en accord avec l'approximation au premier ordre de la valeur que nous avons calculée. Si la condition d'isotropie dans R1 est imposée, la valeur qu'ils donnent pour le décalage de temps est incorrecte mais la valeur du décalage de phase est correcte.