Calcul de l'effet Sagnac en relativité restreinte - Définition

Introduction

Après avoir vu l'effet Sagnac il convient d'en faire une analyse détaillée et rigoureuse dans le cadre de la relativité restreinte.

Effet Sagnac

Nous allons dériver l'effet Sagnac dans le cadre de la relativité restreinte. Cela nous confirmera le fait que la relativité restreinte prédit bien l'anisotropie de vitesse de la lumière dans le repère tournant, anisotropie de vitesse caractéristique de l'effet Sagnac (décalage des instants d'arrivée sur un émetteur-récepteur E de deux signaux lumineux émis en même temps par E se propageant en sens inverse le long de la circonférence d'un disque tournant). Il pourra aussi être utile au lecteur d'étudier la géométrie de l'espace-temps dans les repères tournants afin d'avoir des détails complémentaires.

Le repère R désignera un repère inertiel avec son origine au centre du disque tournant de rayon R. L'émetteur-récepteur E est situé en un point (noté E) de la périphérie du disque. Il est entrainé en rotation avec le disque. Le repère tournant, attaché au disque, sera noté R'.

Nous appellerons R1 le repère inertiel (local) d'origine située en E et se déplaçant à la même vitesse V que E. Dans le voisinage de E, R' va à la même vitesse que R1 pendant un temps infinitésimal. C'est dans le référentiel inertiel tangent R1 que la vitesse relative de la lumière est isotrope (conformément à la Relativité Restreinte) et non dans le repère tournant R'. La confusion entre vitesse relative de la lumière dans le repère tournant R' (vitesse relative dont la définition repose sur la synchronisation relativiste des horloges distantes ayant cours dans le référentiel inertiel R) et vitesse relative de la lumière dans le référentiel inertiel tangent R1 (vitesse relative dont la définition repose sur la synchronisation relativiste ayant cours dans le référentiel inertiel tangent R1) est à l'origine d'erreurs de raisonnement qui ont, dans le passé, conduit à interpréter à tort l'effet Sagnac comme une mise en défaut de la Relativité Restreinte.

R1, R2, R3... désigneront des repères inertiels tangents allant à la vitesse de R' dans un voisinage infinitésimal d'un point du bord du disque tournant (et pendant une durée infime). Les transformations de Lorentz entre repères inertiels peuvent être utilisées alors que pour traiter le cas de R' dans sa globalité la transformation de Lorentz est inapplicable.

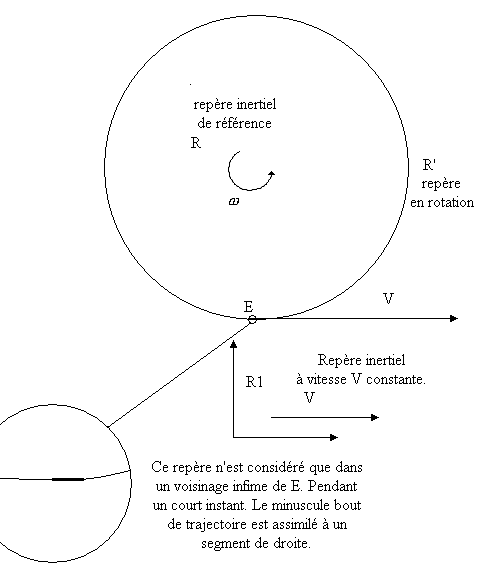
Le disque est en rotation avec la vitesse angulaire ω. Le disque étant plat, à deux dimensions, nous choisissons de travailler en coordonnées polaires .

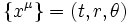
Les coordonnées cartésiennes et polaires sont reliées simplement par :

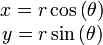
L'intervalle relativiste est donné par

ds² = g_μνdx^μdx^ν = − c²dt² + dr² + r²dθ²

(ici nous avons noté le "tenseur métrique" g_μν car, après le changement de coordonnées, il n'est pas égal au tenseur de Minkowski η_μν). Comme on le vérifie aisément en utilisant le lien entre coordonnées polaires et cartésiennes.

La ligne d'univers de E est donnée par les coordonnées :

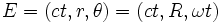
C’est-à-dire

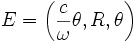
E émet deux signaux S₁ et S₂ (pas nécessairement de la lumière) dont les vitesses angulaires sont ω₁ (signal dans le même sens que E) et ω₂ (signal dans le sens inverse). Leur ligne d'univers est donnée, tout comme ci-dessus, par

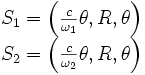
Ce qui nous intéresse est la réception des signaux S₁ et S₂ par E après un tour complet, c’est-à-dire le moment où les lignes d'univers se recoupent. Ces événements ont lieu aux instants

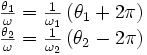
La solution de ce système d'équations est

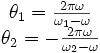
Pour alléger l'écriture, nous allons utiliser les vitesses réduites , et . Les relations précédentes s'écrivent alors

.

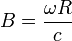
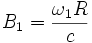
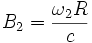
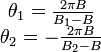
Le temps propre est donné par l'intervalle cdτ = − ds. Par conséquent, pour obtenir le temps propre de E, c’est-à-dire le temps lu par E sur l'horloge au repos dans R', il faut intégrer l'intervalle sur sa ligne d'univers (le long de la circonférence du disque, R' s'identifie localement au cours du temps avec les différents repères inertiels tangents notés R1, R2... dans le voisinage de leur origine).

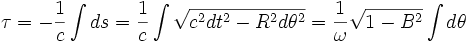
Avec les temps calculés plus haut, nous avons maintenant le temps indiqué par l'horloge de E lors des événements de réception des deux signaux émis par E.

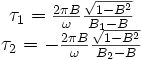
Et la différence est égale à

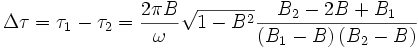
On s'intéresse au cas où l'émetteur-récepteur E utilise des signaux dont la vitesse est isotrope dans R1 (comme des signaux lumineux par exemple). Si E émet des particules, il suffit qu'il les émette de la même manière dans les deux directions. Pour de la lumière se propageant dans un milieu où sa vitesse est inférieure à c (de l'eau, une fibre optique), il faut que le milieu se déplace avec E, c’est-à-dire soit solidaire du disque. De même si on utilise des ondes sonores l'air doit donc se déplacer avec le disque (c'est par rapport au milieu de propagation que la vitesse du son est constante).

Pour imposer les vitesses isotropes dans R1, nous avons besoin de connaître les vitesses B'₁ et B'₂ des signaux dans R1. R et R1 étant des repères inertiels, nous pouvons utiliser l'addition des vitesses et nous avons

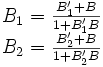
En remplaçant dans la différence de temps, nous obtenons

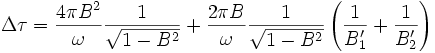
Nous pouvons maintenant tenir compte de la contrainte d'émission avec une vitesse isotrope

B'₁ = − B'₂

La relation précédente devient alors

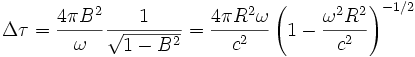
C'est l'effet Sagnac relativiste.

Le calcul de la différence de temps d'arrivée des signaux en E dans R' est donné dans la partie technique. Ce résultat est dérivé en toute généralité puis en supposant que la vitesse des signaux est isotrope dans R1.

Quelques remarques s'imposent.

• Ce résultat est bien identique, au premier ordre près (c’est-à-dire en considérant des vitesses angulaires petites), au résultat obtenu dans l'étude simple de l'effet Sagnac obtenu dans un cadre classique. C'est également le résultat obtenu expérimentalement.
• Ce résultat montre qu'à grande vitesse il y a une correction relativiste typique.
• Même si la vitesse d'émission est isotrope localement dans R1, après un tour complet des signaux, E constate bien un Time Gap donné par la relation dans la partie technique. Ceci confirme l'aptitude de la relativité restreinte à modéliser l'anisotropie de la vitesse de la lumière dans le référentiel tournant.
• La vitesse des signaux n'apparaît pas dans l'expression obtenue. L'effet Sagnac est indépendant de la vitesse des signaux (à condition qu'ils soient isotropes) et ne dépend que de la rotation du disque. L'effet Sagnac est universel. C'est prédit par la relativité restreinte et confirmé expérimentalement.