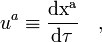Force de Lorentz - Définition

Introduction

Le cercle décrit par le champ magnétique dans un moteur triphasé.

La force de Lorentz, ou force électromagnétique, est la principale manifestation de l'interaction électromagnétique. La force de Lorentz, appliquée dans diverses situations, induit l'ensemble des interactions électriques et magnétiques observées ; elle est de ce fait principalement étudiée en physique et en chimie.

Les effets quantiques affectant la force électromagnétique sont étudiés dans le cadre de l'électrodynamique quantique.

Ordre de grandeur

L'interaction électromagnétique est la deuxième des quatre interactions élémentaires dans l'ordre des puissances. À basse énergie, soit celle des réactions chimiques ou nucléaires, elle est à peu près cent fois plus faible que l'interaction forte, mais dépasse les interactions faibles et gravitationnelles d'un facteur 10¹¹ et 10⁴² respectivement.

Dérivation de la force de Lorentz

On définit comme de coutume en relativité restreinte la quadrivitesse par

ce qui permet de réécrire l'action sous la forme

.

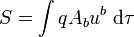
Dans le formalisme de l'action (qui est l'intégrale du lagrangien), la trajectoire est déterminée par la maximisation de l'action par rapport aux variations possibles de la trajectoire x^b(τ). La trajectoire apparaît explicitement dans le quadrivecteur vitesse, mais aussi implicitement dans le quadripotentiel, puisque l'on évalue celui-ci en chaque point de la trajectoire. Ainsi, la variation de l'action donne-t-elle

.

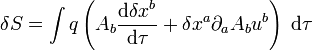
On peut intégrer le premier terme par partie, pour obtenir

,

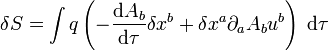
mais comme le quadripotentiel dépend est uniquement évalué sur des points de la trajectoires, on a

.

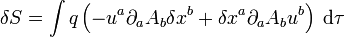
En regroupant l'ensemble des termes, il vient

.

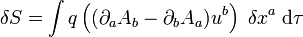
Le terme de l'intégrale en dehors du dτ et des δx^a donne la force. En introduisant le tenseur électromagnétique F tel que

,

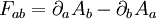
la force f^a s'écrit donc

.

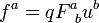
Du fait de la structure des équations de Maxwell, on montre que le champ magnétique peut être écrit sous la forme du rotationnel d'un vecteur, le potentiel vecteur du champ magnétique. Or la partie spatiale du tenseur électromagnétique peut s'écrire, si l'on se place en coordonnées cartésiennes x, y, z,

.

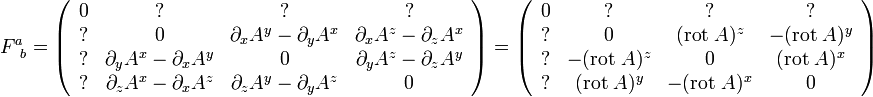
Appliqué à la partie spatiale de la quadrivitesse, on vérifie, en notant B le rotationnel de A, que l'on a

.

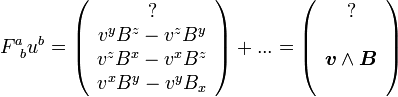
Si maintenant on considère en sus les composantes temporelles du tenseur F, on a

.

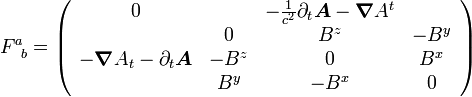
Or, étant données les équations de Maxwell, on sait que l'on peut écrire le champ électrique comme la somme de l'opposé de la dérivée temporelle du potentiel vecteur et du gradient du potentiel électrique, que l'on va assimiler à A. On a ainsi l'expression quadridimensionnelle de la force :

.

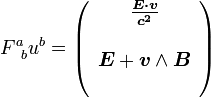
Description mathématique

Champ magnétique dans une bobine.

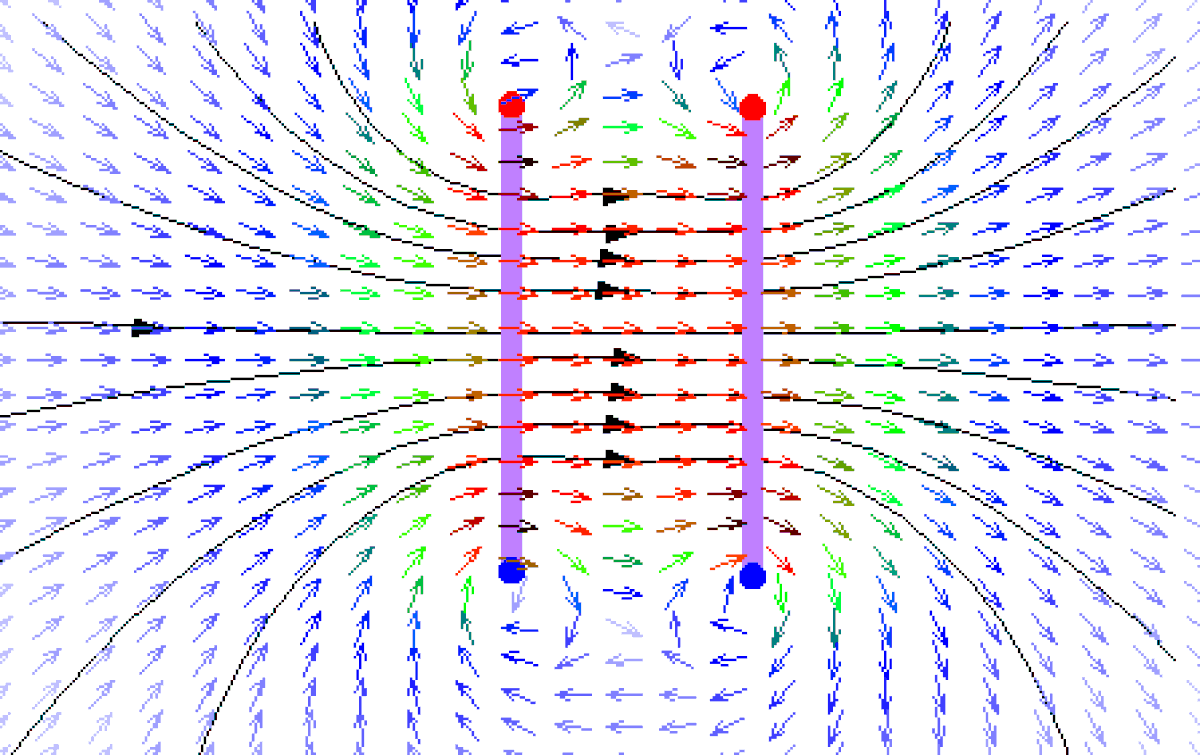
Le champ électromagnétique exerce la force suivante sur des particules possédant une charge électrique q non nulle

,

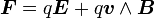
où E et B sont le champ électrique et le champ magnétique pris au point où se trouve la particule, dont la vitesse est v. Le calcul de la force ne se fait que lorsque l'on connaît la valeur des champs E et B, qui sont principalement déterminés par la distribution de l'ensemble des particules chargées intervenant dans la configuration étudiée. En particulier, pour une charge immobile située en r', le champ magnétique est nul et le champ électrique s'exerçant en r est donné par la loi de Coulomb :

,

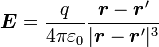
où ε est une constante universelle appelée la permittivité du vide (à remplacer par la permittivité du milieu, lorsqu'on n'est pas dans le vide).

Action de la force de Lorentz dans le cas d'un champ électrique nul.

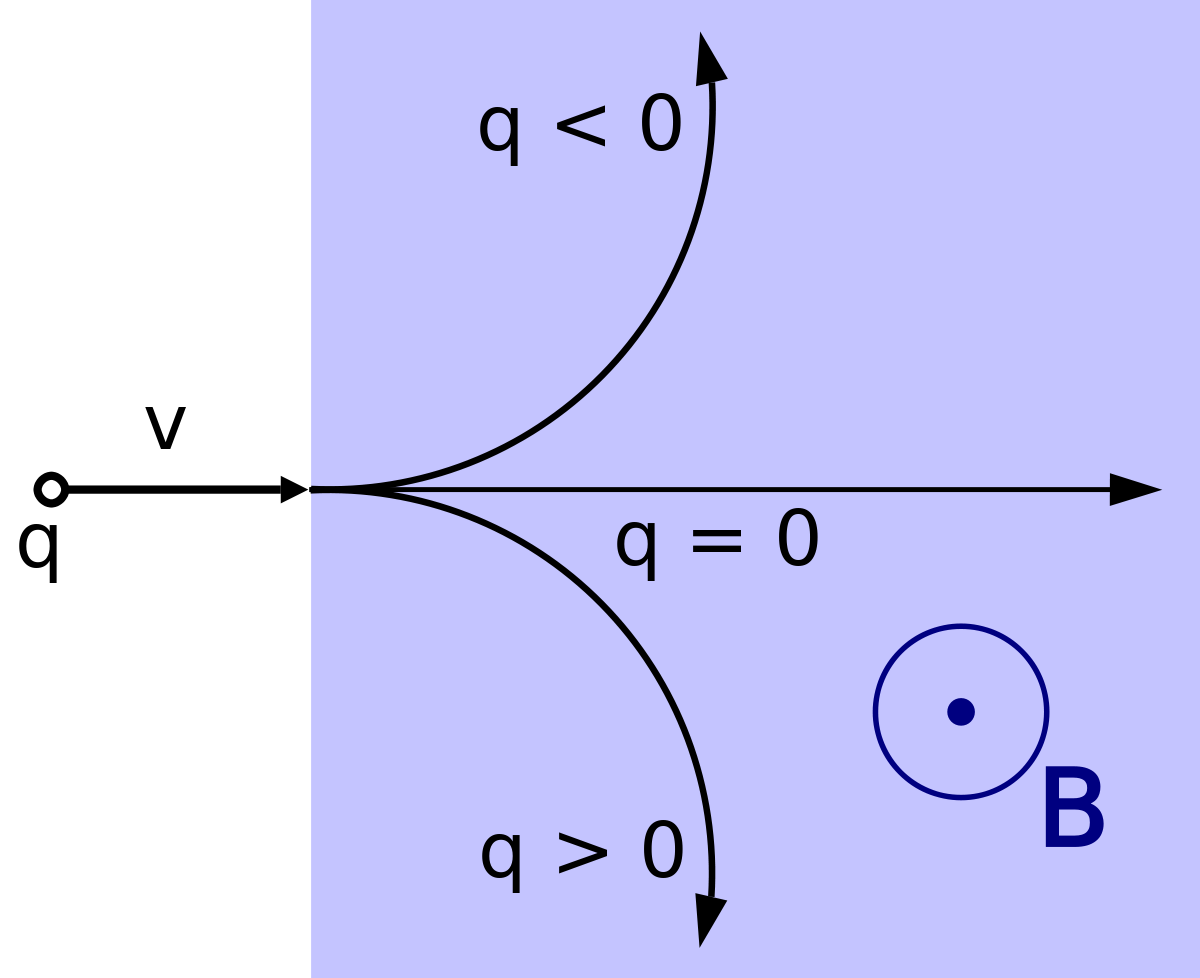
Historiquement, la force de Lorentz était une donnée indépendante de l'équation décrivant le champ électromagnétique. La démonstration de la cohérence interne de la définition de la force de Lorentz se fait sans trop de difficulté dans le cadre du formalisme du lagrangien, appliqué à la relativité restreinte. Dans ce cadre-là, le mouvement d'une particule suivant la trajectoire x^b(τ) soumise au champ électromagnétique est décrit par son action, qui prend la forme

,

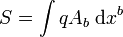
où la quantité A est ce que l'on appelle le quadripotentiel, duquel on tire le potentiel électrique et le potentiel vecteur qui déterminent entièrement le champ électrique et le champ magnétique.