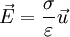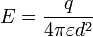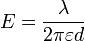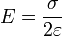Champ électrique - Définition

Approfondissements

Particules créant un champ

Dans la vie courante, ces sources du champ électrique sont la plupart du temps des électrons, chargés négativement, ou des protons, chargés positivement.

Moment dipolaire

Définition

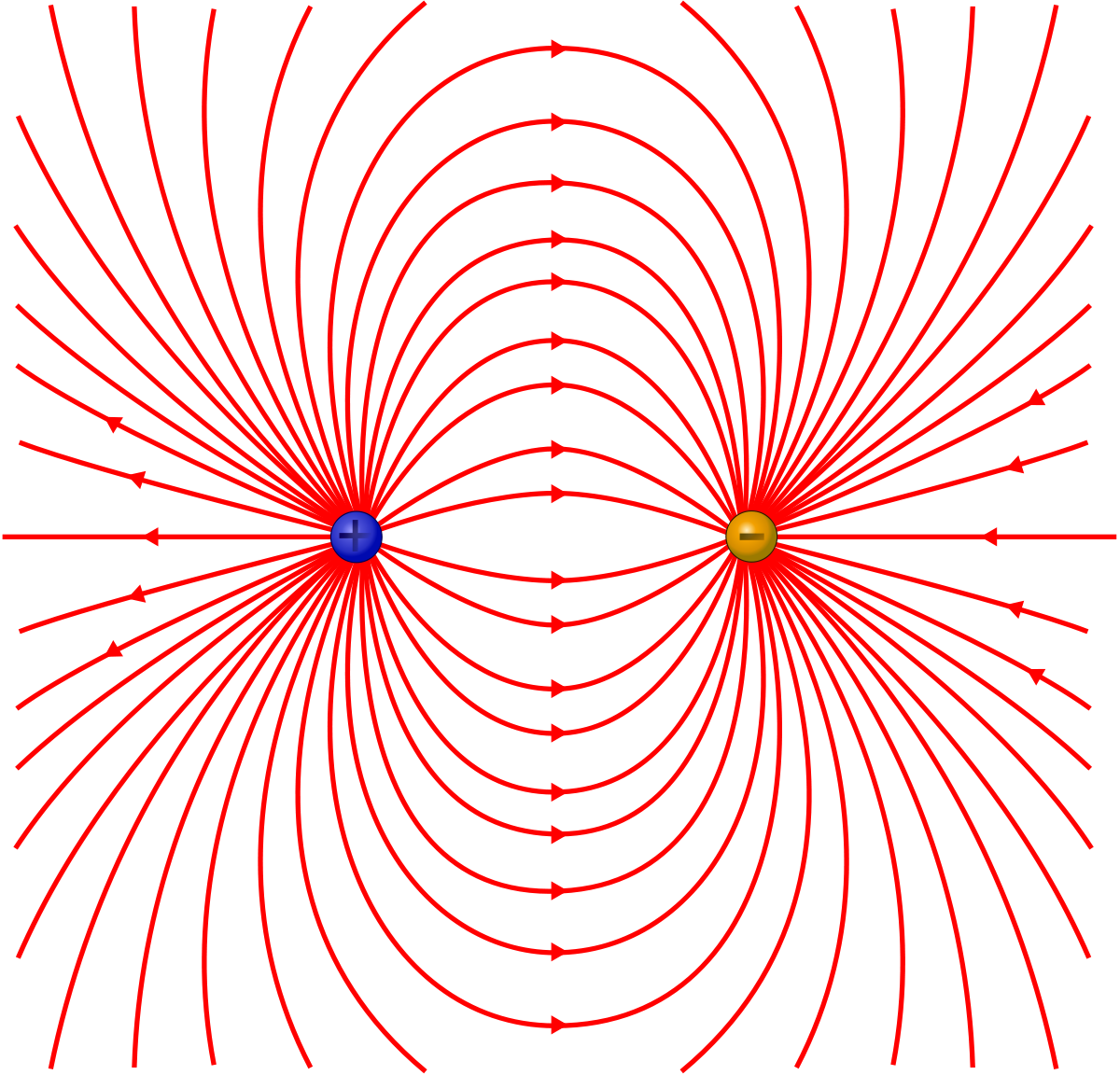
On appelle généralement dipôle électrique un ensemble constitué de deux charges de même valeur, de signes opposées, et placées proches l'une de l'autre (du point de vue de l'observateur). Le moment dipolaire est alors le vecteur , où q est la valeur de l'une des charge (positive) et le vecteur allant de la charge négative à la charge positive.

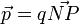
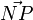
Application aux noyaux atomiques

Lorsque la matière se présente sous forme d'atomes la charge électrique des électrons compense celle des protons qui en constituent le noyau. Si on se place à une distance importante d'un atome par rapport à sa taille, on parle d'échelle macroscopique, ce dernier est donc assimilable à un corps neutre électriquement. Le champ électrique qu'il créé est donc relativement très faible. En astrophysique par exemple, le champ électrique créé par la matière ordinaire qui constitue les planètes est négligeable devant l'influence exercée par cette même matière par l'intermédiaire de la gravitation. Mais bien que les atomes et les molécules soient neutres vus de loin, les charges positives et négatives ne sont pas localisées au même endroit. Si on se place à une distance de l'ordre de la taille de l'atome ou de la molécule, c'est ce qu'on appelle l'échelle microscopique, on s'aperçoit que cette dissymétrie de disposition des charges engendre ce qu'on appelle un moment dipolaire électrique. Un tel dipôle électrique engendre lui aussi un champ électrique mais d'intensité beaucoup plus faible que celle d'une charge électrique. On appelle forces de van der Waals les forces exercées entre les atomes et molécules du fait des champs électriques créés par tous ces dipôles microscopiques.

Champ et localité

La notion de champ électrique, bien que naturelle aujourd'hui, est en réalité assez subtile et est étroitement liée à la notion de localité en physique.

Si on considère une charge électrique source et une charge test placée en un point de l'espace alors la seule quantité effectivement mesurable expérimentalement est la force électrique de la première sur la seconde. Il est important de réaliser qu'a priori la force électrique est donc définie comme une action à distance d'une charge sur une autre. L'avancée conceptuelle de la notion de champ est la suivante: il est possible de remplacer cette action à distance de par l'existence en tout point de l'espace d'une nouvelle quantité, de nature mathématiquement vectorielle, appelée champ électrique et dont la valeur résume l'influence de en chaque point de l'espace. Pour déterminer l'évolution de la charge test il n'est donc plus besoin de se référer constamment à la charge source située au loin mais seulement de lire l'information contenue localement dans le champ électrique à l'emplacement de . La force est alors obtenue selon l'équation

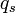
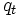
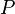
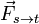
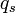
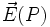
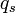
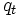
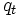
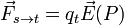
Ce principe de localité n'est absolument pas anodin. En particulier une conséquence non-triviale de celui-ci est que si on considère deux configurations de sources électriques et que par ailleurs on peut montrer qu'en un certain point de l'espace les champs électriques créés par ces deux distributions sont les mêmes alors nécessairement l'effet de ces deux jeux de source en ce point sont absolument indistinguables.

Un exemple de situation où la notion de champ, ou de façon équivalente la localité de la théorie électromagnétique, prend toute son ampleur apparait lorsque se pose la question de déterminer les propriétés de transformation d'un champ électrostatique sous les transformations de Lorentz: considérons un boost de Lorentz donné par un vecteur vitesse et la décomposition du champ électrique . Ce champ est créé par une distribution arbitraire de sources. Par localité, en se limitant au point on peut remplacer la distribution de charges par un condensateur plan contenant et créant un champ électrique uniforme égal à en tout point intérieur à son enceinte(on note la densité surfacique de charge associée).

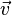
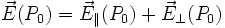
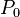
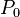
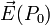
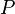
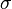
Supposons d'abord que se trouve dans le plan de cette distribution surfacique fictive (ce qui est le cas si le champ électrique est transverse au mouvement) on en déduit que dans le nouveau référentiel,

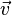
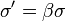
par contraction des longueurs, avec , et donc

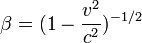
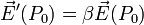
Si par contre le champ est longitudinal alors la distribution surfacique des charges fictives est transverse et donc inaffectée par le changement de référentiel et alors

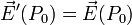
Dans le cas le plus général d'une direction quelconque on a alors par principe de superposition

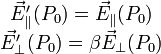
On a donc déduit très simplement le champ électrique dans le nouveau référentiel sans jamais se poser la question de la distribution des sources réelles dans le nouveau référentiel (si la distribution d'origine était compliquée alors reproduire ce résultat de façon directe serait très difficile en général). Insistons enfin encore une fois sur l'absence de champ magnétique dans le référentiel original pour dériver ce résultat.

Exemples simples de calcul du champ électrique

Les quelques exemples qui suivent sont des applications simples du théorème de Gauss.

Champ créé par une charge ponctuelle

Soit une charge ponctuelle q située en un point O. Soit un point de l'espace M. La force induite par le champ électrique provoqué par q en M vaut :

avec : la permittivité du vide qui vaut 8,85.10^-12 C²N^-1m^-2

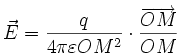
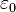
• Le module du champ électrique décroît proportionnellement avec le carré la distance d . Sa direction passe par le point O (champ radial). L'expression de son module à une distance d est :

• L'atténuation de l'effet d'une charge ponctuelle dépend du carré de la distance. L'effet de la charge devant se répartir sur la surface d'une sphère 4πd² qui est d'autant plus étendue que l'on s'éloigne de la charge.

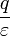
• Si l'on considère la charge créée par une sphère uniformément chargée en un point qui ne lui est pas intérieur (c'est-à-dire que la distance du point au centre O de la sphère est supérieur au rayon de la sphère), le champ créé par cette sphère est alors identique au champ créé par une charge ponctuelle placée en O et de valeur la charge totale de la sphère.

Champ créé par un fil infiniment long et uniformément chargé

• On défini la charge linéique par :

en C.m^-1

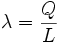
Q étant la charge d'une portion (élément de longueur) du fil et L est la longueur de cette portion

• Le module champ électrique décroît proportionnellement avec la distance d . Sa direction est perpendiculaire au fil et passe par le fil (champ radial). L'expression de son module à une distance d est :

• L'atténuation de l'effet d'un fil infiniment long dépend de la distance. L'effet de la charge devant se répartir sur le périmètre d'un cercle qui est d'autant plus étendu que l'on s'éloigne de la charge.

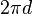
Champ créé par une plaque plane infinie, uniformément chargée

• On définit la charge surfacique par :

en C.m^-2

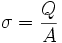
Q étant la charge d'une région (élément de surface) de la plaque et A est la superficie de cette région.

• Le champ électrique créé est uniforme : sa direction est une perpendiculaire au plan et l'expression de son module est la même en tout point de l'espace et elle est indépendante de la position :

Champ créé par un condensateur plan

• L'association de deux plaques planes identiques, parallèles et séparées par une distance d constitue un condensateur plan de capacité :

en F (Farad)

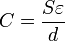
• Le champ électrique à l'intérieur vérifie :

avec σ la charge surfacique portée par les armatures et un vecteur unitaire perpendiculaire aux plaques dans le sens des potentiels décroissants.