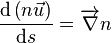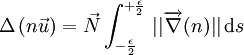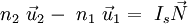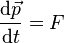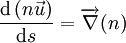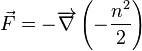Chemin optique - Définition
La liste des auteurs de cet article est disponible ici.
Loi fondamentale de l'optique géométrique
La loi fondamentale de l'optique géométrique est la suivante :
Cette loi exprimée de manière très générale peut se rapporter à une surface séparant deux indices différents. On pose le vecteur N, normal à la surface. Le vecteur grad(n) est porté par N.
Et en posant Is la valeur de l'intégrale
Ce qui rappelle la loi de Snell-Descartes.
Analogie entre l'optique et la mécanique
En mécanique, on écrit
soit
En remarquant l'analogie avec l'équation
On peut écrire que dans les conditions particulières suivantes (en physique des particules, on utilise la valeur c comme unité de vitesse) :
F dérive d'un potentiel qui n'est fonction que de l'indice de réfraction :
On peut pousser l'analogie en rappelant que l'optique géométrique est l'approximation des faibles longueurs d'onde de l'optique ondulatoire.
L'idée générale de cette analogie (pressentie dans les années 1830 par Hamilton, puis reformulée par Louis de Broglie en 1923) est d'associer quantité de mouvement p de la particule et le vecteur d'onde k de l'onde. Le microscope électronique en est une implémentation concrète.