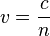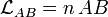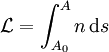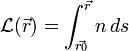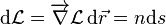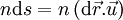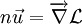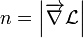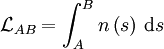Chemin optique - Définition

Introduction

Le chemin optique est un outil de l'optique géométrique et ondulatoire.

Dans un milieu homogène, le chemin optique entre deux points A et B est défini comme la distance AB parcourue par un rayon lumineux multipliée par l’indice de réfraction que le rayon a rencontré lors de son trajet. Cette grandeur a la dimension d'une distance, et plus précisément c'est la distance qu'aurait parcourue la lumière dans le vide pendant la durée qu'elle met à effectuer le trajet dans le milieu donné.

En effet :

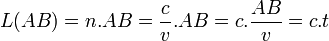
Dans cette équation, c est la vitesse de la lumière dans le vide, v est la vitesse de la lumière dans le milieu joingnant les points A et B, est l'indice de réfraction du milieu (homogène), et est le temps du trajet de la lumière entre A et B.

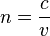
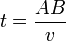
Le principe de Fermat énonce que les trajets empruntés par la lumière pour aller d'un point à un autre ont un chemin optique stationnaire.

Chemin optique et indice de réfraction

Dans les milieux autres que le vide, les propriétés diélectriques des matériaux introduisent une modification de la vitesse de la lumière. La vitesse de la lumière, notée v est liée à l'indice optique n du milieu par la relation :

avec c la vitesse de la lumière dans le vide.

Dans le cas d'un milieu homogène, pour lequel n est le même en tout point, le chemin optique pour aller d'un point A vers un point B en ligne droite, que l'on note , est simplement donné par la distance géométrique entre le point A et le point B multipliée par l'indice de réfraction n. On a ainsi :

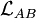
où AB est la distance géométrique entre le point A et le point B.

Exemple : Un rayon lumineux parcourt 5 cm dans une couche d'eau. Parallèlement, un autre rayon lumineux (identique au précédent) traverse 5 cm d'air. L'eau a pour indice de réfraction n = 1,33 et l'air un indice sensiblement égal à celui du vide n = 1. Dans l'eau, le chemin optique du rayon lumineux vaudra D = 1,33 × 5 = 6,65 cm. Dans l'air, il vaudra D' = 1 × 5 = 5 cm. Le chemin optique sera plus long dans l'eau que dans l'air.

S'ils étaient partis en même temps, le rayon lumineux qui traverse l'air arrive "avant" l'autre. cela peut être vérifié avec un laser et des miroirs (un dans l'eau et un dans l'air) par un système d'interférences. La différence de phase entre le rayon ayant traversé de l'eau et celui ayant traversé de l'air sera fonction de la longueur d'eau traversée et du rapport des indices eau/air.

Equation iconale

L'équation iconale (ou eikonale) peut s'obtenir à partir du chemin optique .

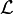
En notant A₀ le point de coordonnées r₀ et A un point générique de coordonnées r situé sur une autre surface d'onde.

Cette notation amène la différentielle suivante :

On peut l'écrire aussi avec le vecteur unitaire u définissant la direction de propagation de l'onde lumineuse.

Ce qui implique l'équation iconale de l'optique géométrique :

avec :

et l'opérateur formel nabla.

Cas général : chemin courbe et milieu inhomogène

Soit une courbe C quelconque, dans un milieu inhomogène (n peut varier en différents points de l'espace). On cherche le chemin optique de la lumière parcourant cette courbe C. Pour cela, on considère deux points eux aussi quelconques appartenant à la courbe C, infiniment voisins et distants d'une distance ds.

Localement, le chemin optique est celui du cas simple : un rayon lumineux en ligne droite. On peut ainsi écrire :

avec n(s) l'indice du milieu en un point s de la courbe. Pour trouver le chemin optique séparant deux points A et B sur cette courbe quelconque, il suffit de faire la somme intégrale de tous les éléments dL sur les coordonnées curvilignes s délimitées par les points A et B :