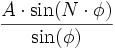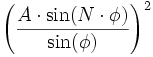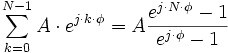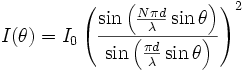Optique ondulatoire - Définition

L'optique ondulatoire est la discipline qui étudie la lumière en la considérant comme étant une onde électromagnétique. L'optique ondulatoire s'attache plus particulièrement aux phénomènes affectant les ondes, comme les interférences et la diffraction.

Principe

La lumière pour aller d'un point à un autre se propage avec une vitesse déterminée. La lumière en un point donné sera l'addition cohérente ou incohérente du champ électromagnétique en ce point à l'instant t. Ce champ est ondulatoire ; cela signifie que la lumière est une onde se propageant avec une certaine vitesse. Cela a de nombreux effets différents de l'optique géométrique. Par exemple, on assiste à des phénomènes d'interférence et de diffraction. Ils se produisent lorsque les sources sont cohérentes entre elles : la façon la plus simple de le faire est d'utiliser une seule source, de la séparer en deux faisceaux, et de les ramener au même endroit.

Exemple

Considérons une onde plane monochromatique arrivant sur N fentes parallèles. Si on néglige les phénomènes de diffraction, l'amplitude totale est donnée par la relation :

L'intensité est égale au carré de l'amplitude :

On a, pour 7 fentes, la courbe :

C'est ainsi que la superposition d'ondes donne des franges sombres (là où l'interférence est destructive) et des franges plus intenses que la simple somme des N sources (là où l'interférence est constructive).

Démonstration 

La formule de la somme d'une suite géométrique nous permet de faire la somme des signaux cohérents issus des N fentes ayant tous A comme amplitude et déphasés chacuns par rapport au suivant de  :

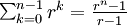
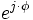
En utilisant la relation de Bragg pour exprimer le déphasage dans la direction θ : , on obtient :

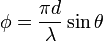
où N est le nombre de fentes, d est la largeur des fentes, λ est la longueur d'onde de l'onde, et θ est la direction de la lumière après passage dans les fentes.

Un cas particuler : les fentes d'Young

Le cas N=2 correspond à deux fentes parallèles. On a alors la courbe suivante:

C'est en fait une sinusoïde. Si on ne considérait pas la lumière comme ondulatoire, on obtiendrait seulement des fentes élargies.