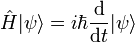Constante de Planck réduite - Définition

Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence Expériences Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect Formalisme Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction Statistiques Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson Théories avancées Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman Interprétations Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

Cette boîte : voir • disc. • mod.

La constante de Planck réduite, ou constante de Dirac (du nom du physicien Paul Dirac), notée ℏ (prononcer « h barre »), est dérivée de la constante de Planck h. Le symbole ℏ correspond au caractère unicode U+210F.

Elle est conventionnellement définie par la formule :

.

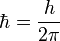
Sa valeur numérique est de

,

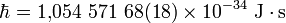
directement tirée de la constante de Planck, qui vaut :

.

est le quantum de moment angulaire, y compris le quantum de spin. C'est-à-dire que le moment angulaire de n'importe quel système, mesuré par rapport à n'importe quel choix particulier d'axe, est toujours un multiple entier de cette valeur. est également utilisée dans le principe d'incertitude de Heisenberg. Pour cette raison, certains pensent que est plus fondamental que h. est employé pour définir les unités de Planck.

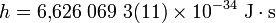
Cette constante est (entre autres) utilisée dans :

• le calcul du spectre électromagnétique du corps noir
• le calcul de la variation de longueur d'onde par la théorie quantique