Continuité - Définition
La liste des auteurs de cet article est disponible ici.
Définition dans le cas des espaces métriques
Définition
Définition — Soient
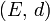
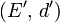
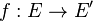
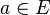
On dit que l'application f est continue en a si :
Ainsi f est continue en a si et seulement si la limite de f en a existe et vaut f(a).
Exemples
- Une application linéaire d'un espace vectoriel normé de dimension finie vers un autre espace vectoriel normé est continue.
- Une application linéaire d'un espace vectoriel normé vers un autre est continue si et seulement si elle est bornée sur la boule unité.
-
- Et en effet, le cas non borné se présente en dimension infinie : considérons comme application linéaire la dérivation sur
![\R[X]](https://static.techno-science.net/illustration/Definitions/autres/6/60ed190117e7614d227f8d1693161a5b_67a4b8800a94a9a175a1ac6f97f6cf7d.png)
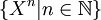
- Et en effet, le cas non borné se présente en dimension infinie : considérons comme application linéaire la dérivation sur
Notion de continuité dans l'histoire
La continuité n'a pas toujours été définie de la façon précédente.
Euler dans son introductio in analysin infinitorum définit la fonction continue comme une fonction définie par une seule expression analytique finie ou infinie (série entière) et appelle fonctions discontinues ou mixtes celles possédant plusieurs expressions analytiques suivant les intervalles. Sylvestre Lacroix (1810) appelle fonction continue une fonction dont toutes les valeurs sont définies à partir d'une même loi ou dépendent d'une même équation. Cette notion de continuité s'appelle la continuité eulérienne et est plus restrictive que la définition actuelle. Par exemple, la fonction définie pour tout réel négatif par f(x) = x et tout réel positif par f(x) = x2 est continue au sens actuel et mixte (discontinue) au sens d'Euler.
La définition que nous utilisons aujourd'hui est celle donné par Bernard Bolzano dans sa théorie des fonctions : « La fonction f(x) varie suivant la loi de continuité pour la valeur x si la différence |f(x + w) - f(x)| peut-être rendue plus petite que toute valeur donnée ».(Prague 1816).
Augustin Louis Cauchy dans son cours d'analyse de l'école royale polytechnique, définit la continuité en x par f est continue en x si la valeur numérique de la différence f(x + a) - f(x) décroit indéfiniment avec celle de a, utilisant ainsi les notions des infiniment petits.
Une autre définition de la continuité, inspirée de celle de Cauchy est de dire que f est continue en a si pour tout suite (xn) convergeant vers a, la suite f(xn) converge vers f(a). Cette définition de la continuité par les suites n'est équivalente à celle actuellement en vigueur que si l'on admet l'axiome du choix.
Malgré cette définition formelle, l'utilisation de la continuité reste au début du XIXe siècle grandement intuitive quand on voit Cauchy tenir le raisonnement suivant, pour démontrer le théorème des valeurs intermédiaires : « La fonction f étant continue entre les points x0 et X, la courbe qui a pour équation y=f(x) sera continue entre les points (x0, f(x0) et (X,f(X)) et la droite d'équation y=b qui passera entre les ordonnées f(x0) et f(X) ne peut que rencontrer dans l'intervalle la courbe mentionnée. »
Il existe aussi une notion de continuité plus forte : la continuité uniforme dans laquelle la distance |f(x) - f(x')| peut être rendue aussi petite que l'on veut pour n'importe quel couple (x, x') tels que la distance |x - x'| soit suffisamment faible. Contrairement à la continuité classique (continuité en un point a fixé), la continuité uniforme assure que la majoration est vraie sans avoir besoin de fixer a. Cette notion fut précisée par Edouard Heine en 1872.
![\forall \varepsilon > 0 \quad \exists \eta > 0 \quad \forall x \in E \quad \Big[d(x,a) \leq \eta \implies d'(f(x),f(a)) \leq \varepsilon\Big]](https://upload.wikimedia.org/math/4/d/a/4da8781585f10a0eb0718186332f1cbe.png)

















































