Continuité uniforme - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En topologie, la continuité uniforme (ou l'uniforme continuité) est une définition plus contraignante que la continuité, et se définit dans les espaces métriques ou plus généralement les espaces uniformes. Contrairement à la continuité, la continuité uniforme n'est pas une notion « purement topologique » c'est-à-dire ne faisant intervenir que des ouverts : sa définition dépend de la distance ou de la structure uniforme.
Définitions et exemples
Espace métrique
Le contexte général de la définition de la continuité uniforme est celui des espaces métriques. Soient (E, d) et (F, δ) deux espaces métriques, et f une application de E dans F.
L'application f est dite uniformément continue si et seulement si :

NB: La continuité « simple » de f s'écrit par comparaison :

Le terme uniforme signifie que le choix de η en fonction de ε ne dépend pas du point considéré, il est uniforme sur E.
Fonction de la variable réelle et à valeurs réelles
Si les espaces de départ et d'arrivée de la fonction f sont des intervalles de l'ensemble des nombres réels munis de la norme valeur absolue, la définition s'écrit :

Exemple et contre-exemple
Soit f1 la fonction qui, à tout réel positif associe sa racine carrée. L'application f1 est uniformément continue. En effet, soit ε un réel strictement positif. La fonction f1 est concave, la majoration suivante est donc vérifiée :
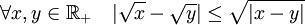
Si η est égal au carré de ε la proposition suivante montre l'uniforme continuité recherchée :
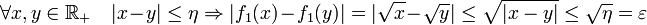
Soit f2 la fonction qui, à tout réel associe son carré. L'application f2 n'est pas uniformément continue. En effet, montrons que :

Il suffit de choisir ε égal à un. Pour tout η strictement positif, soit x (resp. y) le réel égal à 1/η + η (resp. 1/η) Alors :

Ce qui termine la démonstration.
Remarque : La fonction racine carrée est une fonction 1/2-höldérienne. Plus généralement, pour tout
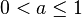
Applications
Approximation uniforme des fonctions continues par les fonctions en escalier
Soit f une fonction continue sur un segment [a, b] et soit ε un réel strictement positif. Alors il existe une fonction en escalier φ sur [a, b], telle que :
![\forall x \in [a,b], |f(x) - \varphi(x)| < \varepsilon](https://static.techno-science.net/illustration/Definitions/autres/c/ca27ab662e6fd8b59a1ebf45a1131ae6_e5d58029ade2d3c8d8542e629f404180.png)
On utilise pour cela le fait que f est uniformément continue (théorème de Heine), et on découpe l'intervalle [a, b] en n sous-intervalles de longueur b - a/ n inférieure au η intervenant dans la définition de l'uniforme continuité. On montre alors que la fonction φ valant f(a + k( b - a)/ n) sur l'intervalle [a + k(b - a)/ n, a + (k + 1)(b - a)/ n] convient.
Intégrale de Riemann
Soit E l'espace vectoriel des fonctions bornées sur l'intervalle [a, b], muni de la norme de la convergence uniforme. Soit F le sous-espace des fonctions en escalier sur [a, b]. Il est aisé de définir l'intégrale I(φ) d'une telle fonction en escalier φ, au moyen d'une somme finie :
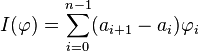
Si φ est constante égale à φi sur l'intervalle ]ai, ai+1[, les ai constituant une subdivision de [a, b]. On montre alors que I est une fonction lipschitzienne sur F, donc uniformément continue, elle se prolonge à l'adhérence de F dans E. Cette adhérence constitue l'espace des fonctions réglées, et contient les fonctions continues. On a défini ainsi l'intégrale de Riemann des fonctions réglées.
Approximation des fonctions continues par les polynômes
Soit f une fonction bornée sur [0, 1]. Considérons la suite de polynômes :
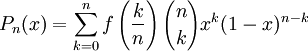
Si f est continue en x, on montre que la suite (Pn(x)) converge vers f(x). Si f est continue sur [0, 1] et donc uniformément continue, on montre que la suite (Pn) converge uniformément vers f sur [0, 1]. Ce résultat constitue une version constructive du théorème de Stone-Weierstrass.
Espace vectoriel normé
Un espace vectoriel normé n'est pas nécessairement complet. Or la complétude se révèle une propriété importante pour l'étude d'espaces fonctionnels. Elle permet par exemple d'utiliser le théorème de Hahn-Banach ou de Banach-Steinhaus.
Il existe une technique permettant de compléter un espace métrique (cf Espace complet). Appliquée à un espace vectoriel normé (cf Complété d'un espace vectoriel normé), elle produit un espace qui est non seulement un espace métrique complet mais un espace vectoriel normé complet, encore appelé espace de Banach. La propriété générale de prolongement par continuité (vue plus haut) devient alors utile pour comparer les applications linéaires continues sur E et celles sur son complété. Ces techniques restent valables pour un espace muni d'un produit scalaire.