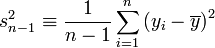Convergence de variables aléatoires - Définition
La liste des auteurs de cet article est disponible ici.
Convergence en probabilité
Définition — On dit que Xn converge vers X en probabilité si,
La convergence en probabilité est parfois notée
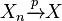
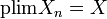
La convergence en probabilité est utilisée dans la loi faible des grands nombres.
La convergence en probabilité implique la convergence en loi. On peut donc énoncer le théorème suivant:
Théorème — Xn converge vers X en probabilité
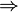
Pour effectuer la démonstration, le lemme suivant est utile
Soient X, Y des variables aléatoires réelles, c un réel et ε > 0. Alors
Lemme — 
car
Pour tout ε > 0, en raison de ce lemme, on a:
On a donc
Soit a un point de continuité de FX. On fixe un réel 
. Par continuité de FX en a, il existe un réel 
tel que
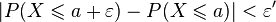
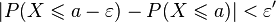
De la convergence de (Xn)n en probabilité vers X, on peut en déduire l'existence d'un entier N tel que : 
.
D'où :
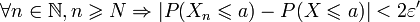
Il existe des conditions suffisantes de convergence en probabilité vers une constante, portant sur l'espérance et la variance des termes de la suite :
Théorème —
![\lim_{n \to \infty} \operatorname{E}[X_n]=c\quad \mathbf{ et } \quad \lim_{n \to \infty}\operatorname{Var}[X_n]= 0 \Rightarrow X_n \xrightarrow{p} c](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/2a6f6e8ad2edf8576f817d4530e0072b_136af4fe1d79280977544480233af275.png)
On veut montrer que
On se sert de l'inégalité de Markov pour les variables aléatoires réelles admettant un moment d'ordre 2 :
Théorème — ![\mathbb{P}\left(\left|U\right| \geq \varepsilon \right) \leq \frac{\operatorname{E}\left[U^2\right]}{\varepsilon^2}\qquad \forall \varepsilon >0.](https://upload.wikimedia.org/math/2/b/9/2b9f00e50d186db7d53e13acbb0b5f3a.png)
D'où :
![\begin{align} \mathbb{P}\left(\left|X_n-c\right| \geq \varepsilon \right) &\leq \frac{\operatorname{E}\left[(X_n-c)^2\right]}{\varepsilon ^2}\\ &= \frac{\operatorname{Var}(X_n-c)+\left(\operatorname{E}[X_n-c]\right)^2}{\varepsilon ^2}\text{ (formule de Huygens)}\\ &= \frac{\operatorname{Var}(X_n)+\left(\operatorname{E}[X_n]-c\right)^2}{\varepsilon ^2}\\ \end{align}](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/21eb531a6992254fc1ea61641487bf9f_408e739eeeb07ec850cb7204539b7b8f.png)
Il en découle que :
si
![\operatorname{E}[X_n]\to c \quad \mathbf{ et }\quad \operatorname{Var}[X_n]\to 0\text{ alors }\mathbb{P}\left( |X_n -c|\geq\varepsilon\right)\to 0,\text{ donc } X_n \xrightarrow{p} c](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/020a324e9656aa809e9f5ddc09eb7de4_2ad4163f7a1b9c78b4ac907d9084c5d2.png)
Ce théorème est très utile pour démontrer la loi faible des grands nombres de manière simple: il suffit de voir que si
-
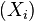
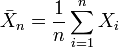
![\operatorname{E}[\bar{X}_n]=\mu](https://static.techno-science.net/illustration/Definitions/autres/2/22bcfe41117d0857580c71852d74eb12_1db1b653e02decc880d937e1d65520f8.png)
-
![\lim_{n\to\infty}\operatorname{Var}[\bar{X}_n]=\lim_{n\to\infty}\frac{\sigma^2}{n}=0\qquad](https://static.techno-science.net/illustration/Definitions/autres/8/873308dd3c766f52264fc3242c3d6203_400abb9e024dfc7f89b270681b2f009b.png)
![\operatorname{E}[\bar{X}_n]=\mu](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/22bcfe41117d0857580c71852d74eb12_1db1b653e02decc880d937e1d65520f8.png)
![\lim_{n\to\infty}\operatorname{Var}[\bar{X}_n]=\lim_{n\to\infty}\frac{\sigma^2}{n}=0\qquad](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/873308dd3c766f52264fc3242c3d6203_400abb9e024dfc7f89b270681b2f009b.png)
Donc
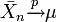
La réciproque n'est pas vraie :
- En statistiques, un estimateur peut être biaisé mais cependant convergent !
- Dans l'exemple suivant, la suite, d'espérance constante, converge vers une constante différente de cette espérance ; la suite des variances tend vers l'infini.
Soit une suite
-
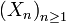
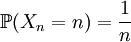
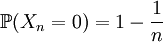
On voit qu'elle converge en probabilité : 
.
Cependant,
![\operatorname{E}[X_n]=1](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/e97947bace53c8f30865c87398f213e9_312887db552807673ab0be117cfebbf9.png)
![\operatorname{Var}[X_n]=n-1\to +\infty](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a58df8265cbaa761b1c87a120f28d62e_c5f8f2c1c576d9fa9a007bc8f183bf16.png)
Ainsi les conditions énoncées plus haut de convergence en probabilité vers une constante ne sont pas nécessaires.
Convergence d'une fonction d'une variable aléatoire
Un théorème très pratique, désigné en anglais généralement sous le nom de Mapping theorem (en), établit qu'une fonction g continue appliquée à une variable qui converge vers X convergera vers g(X) pour tous les modes de convergence:
Théorème — Mapping theorem Soit
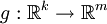
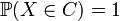
- Si
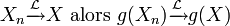
- Si
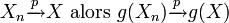
- Si
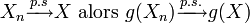
En statistiques, un estimateur convergent de la variance σ2 est donné par:
On sait alors par le continuous mapping theorem que l'estimateur
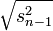
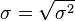
Convergence en moyenne d'ordre r
Soit r > 0. On dit que Xn converge vers X en moyenne d'ordre r ou en norme Lr si E|Xn|r < ∞ pour tout n et
-
-
-
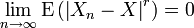
La convergence en moyenne d'ordre r nous dit que l'espérance de la puissance r-ième de la différence entre Xn et X converge vers zéro.
Pour r =2, on parle de convergence en moyenne quadratique
Théorème — Xn converge vers X en norme Lr
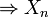
On se sert de l'inégalité de Markov pour les variables aléatoires réelles admettant un moment d'ordre r :
Théorème — ![\mathbb{P}\left(\left|U\right| \geq \varepsilon \right) \leq \frac{\operatorname{E}\left[|U|^r\right]}{\varepsilon^r}\qquad \forall \varepsilon >0.](https://upload.wikimedia.org/math/9/6/f/96f43047765d306e6f6e67c5723839d3.png)
On a donc : , d'où découle le résultat annoncé.
Théorème — Pour r > s ≥ 1, la convergence en norme Lr implique la convergence en norme Ls.
On a également le résultat suivant:
Théorème — Xn converge vers une constante c en moyenne quadratique
![\Leftrightarrow \left\{\lim_{n \to \infty}\operatorname{E}[X_n]=c\quad\mathbf{et}\quad \lim_{n \to \infty}\operatorname{Var}[X_n]=0\right\}](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/f232b573c7bdc039f724c9db7836f2bd_c4334a7ec4dd85068151f1c29cbc96f1.png)
On a vu plus haut que :
![\operatorname{E}\left[(X_n-c)^2\right] = \operatorname{Var}(X_n)+\left(\operatorname{E}[X_n]-c\right)^2](https://static.techno-science.net/illustrationWebp/Definitions/autres/3/35ddd76e71c05d3143965ea777a403bd_f31962152c22395b7760e38f0986fdb5.png)
