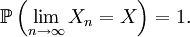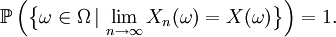Convergence de variables aléatoires - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans la théorie des probabilités, il existe différentes notions de convergence de variables aléatoires. La convergence (dans un des sens décrits ci-dessous) de suites de variables aléatoires est un concept important de la théorie des probabilités utilisé notamment en statistique et dans l'étude des processus stochastiques. Par exemple, la moyenne de n variables aléatoires indépendantes et identiquement distribuées converge presque sûrement vers l'espérance commune de ces variables aléatoires. Ce résultat est connu sous le nom de loi forte des grands nombres.
Dans cet article, on suppose que (Xn) est une suite de variables aléatoires réelles, que X est une variable aléatoire réelle, et que toutes ces variables sont définies sur un même espace probabilisé
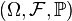
Convergence en loi
Soient F1, F2, ... la suite des fonctions de répartition associées aux variables aléatoires réelles X1, X2, ..., et F la fonction de répartition de la variable aléatoire réelle X. Autrement dit, Fn est définie par Fn(x)=P(Xn ≤ x), et F par F(x)=P(X ≤ x).
La suite Xn converge vers X en loi, ou en distribution, si
-
-
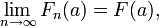
-
Puisque F(a) = P(X ≤ a), cela signifie que la probabilité que X appartienne à un certain intervalle est très similaire à la probabilité que Xn soit dans cet intervalle pour n suffisamment grand. La convergence en loi est souvent notée en ajoutant la lettre
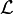
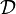
La convergence en loi est la forme la plus faible au sens où, en général, elle n'implique pas les autres formes de convergence définies ci-dessous, alors que ces autres formes de convergence impliquent la convergence en loi. C'est ce type de convergence qui est utilisé dans le théorème de la limite centrale.
De manière équivalente, la suite (Xn) converge en loi vers X si et seulement si pour toute fonction continue bornée
Théorème de continuité de Paul Lévy — Soit
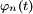
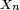
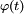
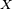
Autrement dit, (Xn) converge en loi vers X ssi la fonction caractéristique de la variable aléatoire réelle Xn converge simplement vers la fonction caractéristique de la variable aléatoire réelle X.
La moyenne d'une suite de variables aléatoires centrées, indépendantes et de même loi, une fois renormalisée par
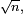
La loi de Student de paramètre


Dans ce cas, on peut aussi utiliser le lemme de Scheffé, qui est un critère de convergence d'une suite de variables aléatoires à densité vers une variable aléatoire à densité.
La suite
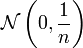
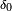
Convergence presque sûre
On dit que Xn converge presque sûrement ou presque partout ou avec probabilité 1 ou fortement vers X si
Cela signifie que les valeurs de Xn approchent la valeur de X, au sens où (cf. presque partout) l'événement sur lequel Xn ne converge pas vers X a une probabilité nulle.
On note souvent cela ou
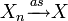
On peut expliciter la définition de la convergence presque sûre en utilisant l'espace probabilisé
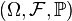

Théorème — Xn converge vers X presque sûrement
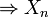
La convergence presque sûre est utilisée dans la loi forte des grands nombres.
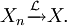
![\lim_{n\rightarrow\infty} E[f(X_n)]=E [f(X)].](https://static.techno-science.net/illustration/Definitions/autres/4/4df277188d111e3ffb3a55fbcc53e237_10bb4adb52ba4f71543d5c8ff0a0adf4.png)
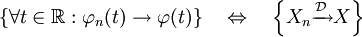
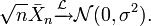
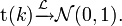
![\mathbb{P}(X_0\le x)=\delta_0\left(]-\infty,x]\right)=\begin{cases}0 & \text{ si } x< 0,\\1 &\text{ si } x \geq 0.\end{cases}](https://static.techno-science.net/illustration/Definitions/autres/5/558cc28ff14794779ac82a1bf2e028e1_ad8d1907094841dc7227a9977ff0a376.png)