Convolution de Dirichlet - Définition

Fonction multiplicative

Groupe des fonctions multiplicatives

L'anneau des fonctions arithmétiques n'est pas un corps.

• Le groupe des unités de l'anneau des fonctions arithmétiques est composé des fonctions ayant une image de 1 non nulle.

Le groupe des unités est constitué des éléments ayant un inverse pour le produit de Dirichlet. Les fonctions multiplicatives, par définition, ont pour image de 1 la valeur 1. Elles sont donc toutes inversibles. De plus :

• L'ensemble M des fonctions multiplicatives, muni de la convolution de Dirichlet, forme un groupe abélien.

En conséquence, le produit de deux fonctions multiplicatives est multiplicatif.

• Toute fonction arithmétique f ayant pour image de 0 une valeur différente de 0 est inversible pour la convolution :

Soit g la fonction définie par récurrence de la manière suivante :

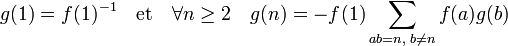
Par construction, (f * g(1)) = 1. Cette égalité, ainsi que le calcul suivant démontre la proposition.

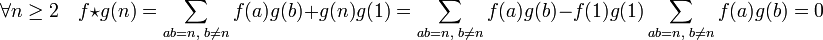
• L'ensemble des fonctions multiplicatives muni de la convolution est un groupe abélien :

L'associativité, la commutativité et l'existence d'un élément neutre sont déjà établis. Il suffit de démontrer que la convolution de deux fonctions multiplicatives f * g est multiplicative et que l'inverse pour la convolution d'une fonction multiplicative est aussi multiplicative.

Montrons tout d'abord que le produit f * g est multiplicatif. Si p est un nombre premier, s un entier strictement positif et n un entier strictement positif, premier avec p, il suffit de montrer que :

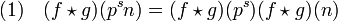
Une récurrence sur le nombre de facteurs premiers de m, un entier strictement positif, montre alors que (f * g)(m.n) = (f * g)(m)(f * g)(n). L'égalité (1) résulte du calcul suivant :

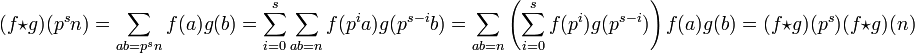
Soit f * la fonction multiplicative égale à l'inverse de f sur les puissances des nombres premiers. La convolution de f * et de f est une fonction multiplicative, égale à 1_F sur les puissances des nombres premiers. La seule fonction multiplicative vérifiant cette propriété est 1_F, ce qui montre que f * est bien l'inverse de f pour la convolution.

 

Fonction de Möbius

La fonction de Mobius, généralement notée μ est définie par l'équation : Id = c₁ * μ. C'est donc l'inverse de la fonction constante 1. Un calcul montre que si n est entier strictement positif sans facteur carré et si k est le nombre de nombres premiers qui divise n, μ(n) = (-1)^k. Si un carré parfait différent de 1 divise n, μ(n) = 0.

L'inverse de la fonction constante 1 joue un rôle particulier, vis à vis de la convolution. Soit f une fonction arithmétique et g une fonction définie par l'égalité g = c₁ * f. La fonction μ permet d'obtenir une expression de f à l'aide de g, plus exactement f = μ * g. Cette égalité est obtenue en appliquant une convolution par μ sur l'égalité définissant g. Ce résultat porte le nom de formule d'inversion de Möbius.

Un exemple d'usage de la formule est son application sur l'indicatrice d'Euler. Cette fonction vérifie l'égalité Id = c₁ * φ. La formule d'inversion montre que :

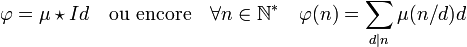
Fonction totalement multiplicative

Une fonctions f est dite totalement multiplicative si elle vaut 1 en 1 et si :

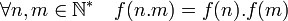
Les fonctions totalement multiplicatives jouent un rôle en arithmétique. En théorie algébrique des nombres les caractères de Dirichlet sont des fonctions totalement multiplicatives. Leurs usages est à la base de la démonstration du théorème de la progression arithmétique de Dirichlet, à l'origine du développement du concept de la convolution de l'article. En théorie analytique des nombres, les fonctions f_s, qui à n associe n^s, où s est un nombre complexe, sont utilisées pour étudier la fonction zêta de Riemann ainsi que la fréquence de certains nombres particuliers, comme les nombres premiers.

Le calcul de l'inverse pour la convolution de ces fonctions est particulièrement aisé :

• Soit f une fonction totalement multiplicative, son inverse est la fonction μ.f, qui à un entier strictement positif n associe μ(n).f(n).

La démonstration est la conséquence du calcul suivant :

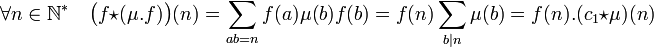
Par définition, la fonction c₁ * μ est égal à 1_F l'élément neutre, ou encore la fonction qui vaut 1 en 1 et 0 partout ailleurs. Il suffit alors de remarquer que f(1) est égal à 1 pour conclure.

Si la convolution de deux fonctions totalement multiplicatives est multiplicative, en revanche elle n'est pas nécessairement totalement multiplicative. Par exemple la convolution c₁ * c₁ correspond à la fonction qui à n associe son nombre de diviseurs. Cette fonction arithmétique n'est pas totalement multiplicative, l'image de 2 est égale à 2 et celle de 4 à 3.