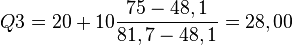Critère de position - Définition

Quartiles

Les quartiles sont les trois valeurs qui partagent la population en 4 sous-populations de même taille

Cas de la variable discrète

On range les valeurs par ordre croissant.

On détermine le second quartile qui correspond à la médiane. Puis on cherche la médiane de la première moitié de la population qui correspond au 1^er quartile. On cherche la médiane de la seconde moitié de la population qui correspond au troisième quartile.

Si la population est de taille n, on distingue 4 cas.

Si n = 4p

Q1 = moyenne entre la p^e et (p+1)^e valeur.

Q2 = moyenne entre la (2p)^e valeur et la (2p+1)^e valeur.

Q3 = moyenne entre la (3p)^e valeur et la (3p+1)^e valeur.

Exemple : série de 12 notes: 4, 5, 7, 8, 8, 9, 10, 10, 10, 11, 13, 16

Q1 = 7,5

Q2 = 9,5

Q3 = 10,5

Si n = 4p+1

Q1 = (p+1)^e valeur.

Q2 = (2p+1)^e valeur.

Q3 = (3p+1)^e valeur.

Exemple : série de 13 notes 4, 5, 7, 8, 8, 9, 10, 10, 10, 11, 12, 13, 16

Q1 = 8

Q2 = 10

Q3 = 11

Si n = 4p+2

Q1 = (p+1)^e valeur.

Q2 = moyenne entre la (2p+1)^e valeur et la (2p+2)^e valeur.

Q3 = (3p+2)^e valeur.

Exemple : série de 14 notes 4, 5, 7, 8, 8, 9, 9, 10, 10, 10, 11, 12,13, 16

Q1 = 8

Q2 = 9,5

Q3 = 11

Si n = 4p+3

Q1 = (p+1)^e valeur.

Q2 = (2p+2)^e valeur.

Q3 = (3p+3)^e valeur.

Exemple : série de 15 notes 4, 5, 7, 8, 8, 9, 9, 10, 10, 10, 11,11, 12, 13, 16

Q1 = 8

Q2 = 10

Q3 = 11

Approximation utile pour une variable discrète

On range les valeurs par ordre croissant.

Q1 est la première valeur pour laquelle l'intervalle [x min, Q1] regroupe au moins 25% de la population.

Q2 est la première valeur pour laquelle l'intervalle [x min, Q2] regroupe au moins 50% de la population.

Q3 est la première valeur pour laquelle l'intervalle [x min, Q3] regroupe au moins 75% de la population.

En reprenant les exemples précédents:

Si n = 12: 25% de n = 3, puis 50% de n = 6, puis 75% de n =9.

La série de notes est 4, 5, 7, 8, 8, 9, 10, 10, 10, 11, 13, 16

Q1 = 7, Q2 = 9, Q3 = 10

Si n = 13: 25% de 13 = 3,25, puis 50% de 13 = 6,5, puis 75% de 13 = 9,75 que l'on arrondit à l'entier supérieur.

La série de notes est 4, 5, 7, 8, 8, 9, 10, 10, 10, 11, 12, 13, 16

Q1 = 8, Q2 = 10, Q3 = 11

On s'aperçoit que cette approximation rend dissymétrique la définition, que le second quartile ne correspond plus à la médiane et que les valeurs obtenues diffèrent de celles de la définition précédente. Son avantage est de rendre la recherche des quartiles (approchés) plus facile sans que l'on soit obligé de distinguer 4 cas. Les différences obtenues par l'une ou l'autre des méthodes se révèlent négligeables et justifient l'usage de cette approximation.

Cas de la variable continue

On calcule les quartiles comme la médiane, graphiquement grâce au polygone des fréquences cumulées croissantes, et par interpolation linéaire grâce au tableau correspondant.

Utilisation du polygone des fréquences cumulées croissantes

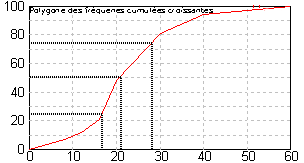
Les droites d'équation, y = 25, y = 50 et y = 75 coupent le polygone en des points dont les abscisses valent environ 17, 21, 28.

Utilisation du tableau des fréquences cumulées croissantes

Le tableau des fréquences cumulées croissantes est :

xi	0	8	12	16	20	30	40	60
fréquences cumulées croissantes	0	7	12,3	21,1	48,1	81,7	94,7	100

25% est atteint dans l'intervalle [16;20] soit pour une valeur de Q1 obtenue par interpolation linéaire .

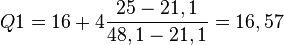
Q2 =M =20,56.

75% est atteint dans l'intervalle [20;30] soit pour une valeur de Q3 obtenue par interpolation linéaire .