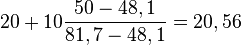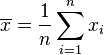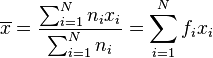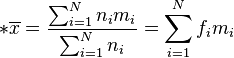Critère de position - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Algèbre |
| Logique |
| Arithmétique |
| Probabilités |
| Statistiques |
Les critères de position d'un ensemble (de valeurs numériques d'un caractère statistique donné) sont quelques valeurs calculées caractérisant globalement la position de cet ensemble, par exemple sa moyenne, son mode, sa médiane, ou ses quantiles (quartiles, déciles) Dans le jargon mathématique belge, on les appelle aussi les valeurs centrales.
En statistiques, on est en général en présence d'un grand nombre de valeurs. Or, si l'intégralité de ces valeurs forme l'information, il n'est pas aisé de manipuler plusieurs centaines voir milliers de chiffres, ni d'en tirer des conclusions. Il faut donc calculer quelques valeurs qui vont permettre d'analyser les données.
En mesure physique (métrologie), on va en général calculer deux valeurs : la moyenne, qui représentera la « valeur » de la mesure, et l'écart type, qui va estimer l'erreur de mesure. Dans d'autres domaines, on va vouloir avoir une description plus fine de la répartition des valeurs, et donc calculer d'autres positions.
Valeur maximum et valeur minimum
La valeur maximale est la plus grande valeur prise par le caractère statistique.
La valeur minimale est la plus petite valeur prise par le caractère statistique.
Moyenne
Cas de la série statistique discrète triée mais non regroupée
L'article Statistiques élémentaires discrètes explique cette formule.
Cas de la série statistique discrète regroupée
L'article Statistiques élémentaires discrètes explique cette formule.
Cas de la série continue
L'article Statistiques élémentaires continues explique cette formule.
Stabilité par transformation affine
La moyenne est stable par transformation affine, c'est-à-dire : si yi = axi + b, si
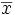
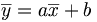
Cette propriété est utile pour changer d'unité: si on connaît une moyenne de température en degré Fahrenheit, il est inutile de convertir toutes les valeurs en degrés Celsius pour calculer la moyenne en degrés Celsius, il suffit de ne convertir que la moyenne.
Il est aussi intéressant, pour limiter la taille des nombres, de partir d'un moyenne estimée et de calculer la moyenne des di = xi − Mestim.. Alors
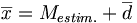
Découpage en sous-population
Si la population est découpée en deux sous-populations P1 et P2 de tailles n1 et n2, si la moyenne du caractère statistique pour la population P1 est
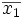
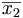
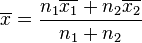
Sensibilité aux valeurs extrêmes
La moyenne est sensible aux valeurs extrêmes ou aberrantes.
Exemple: dans une entreprise, 9 salariés sont payés 2000 Euros mensuels. Le patron se paie 22000 Euros mensuels.
Effectuer la moyenne dans ces conditions conduit à une valeur non représentative:
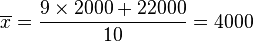
Pour éviter ce genre de piège, il arrive que l'on tronque volontairement la population et qu'on élimine 10% des valeurs les plus basses et 10% des valeurs les plus hautes.
Médiane
La médiane tend à partager la population en deux populations de taille égale. Si m est la médiane, le nombre d"individus dont le caractère statistique est inférieur à m doit correspondre au nombre d'individus dont le caractère statistique est supérieur à m. Si cette définition s'accorde bien avec le cas d'une variable continue, elle n'est pas adaptée au cas d'une variable discrète où une autre définition est donnée. Si les valeurs du caractère statistique sont toutes différentes, la médiane, telle qu'elle est définie dans le cas discret, partage bien la population en deux, mais ce n'est pas toujours le cas si certaines valeurs du caractère statistique sont prises plusieurs fois.
Cas de la variable discrète
On trie les valeurs par ordre croissant.
- Si la population comporte n individus et si n est impair alors n = 2p+1, la médiane sera la (p+1)e valeur du caractère statistique.
- Exemple: série de 13 notes 4, 5, 7, 8, 8, 9, 10, 10, 10, 11,12, 13, 16.
- Médiane = M = 10
- Si la population comporte n individus et si n est pair alors n = 2p, la médiane sera la moyenne entre la pe et (p+1)e valeur du caractère statistique.
- Exemple: série de 12 notes: 4, 5, 7, 8, 8, 9, 10, 10, 10, 11, 13, 16.
- Médiane = M = 9,5
Cas de la variable continue
On utilise le polygone des fréquences cumulées croissantes et le tableau correspondant et on détermine graphiquement ou par interpolation linéaire la valeur M pour laquelle la fréquence de l'intervalle [valeur min, M] vaut 50%.
Utilisation du polygone des fréquences cumulées croissantes
Dans l'exemple développé dans statistiques élémentaires continues, le polygone des fréquences cumulées est le suivant:
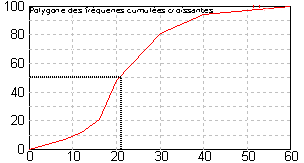
La droite d'équation y = 50 coupe le polygone environ au point d'abscisse 21. M
Remarque: Le polygone des fréquences cumulées croissantes et celui des fréquences cumulées décroissantes se coupent exactement en un point dont l'abscisse est la médiane.
Utilisation du tableau des fréquences cumulées croissantes
Dans l'exemple précédent, le tableau des fréquences cumulées croissantes est :
| xi | 0 | 8 | 12 | 16 | 20 | 30 | 40 | 60 |
| fréquences cumulées croissantes | 0 | 7 | 12,3 | 21,1 | 48,1 | 81,7 | 94,7 | 100 |
Les 50% sont atteint entre 20 et 30 donc pour une valeur M que l'on estime à