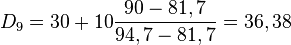Critère de position - Définition
La liste des auteurs de cet article est disponible ici.
Mode
Le mode est la valeur du caractère statistique qui apparaît le plus fréquemment.
| notes xi | 5 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 16 | Total |
| effectifs ni | 1 | 1 | 2 | 4 | 3 | 2 | 1 | 1 | 1 | 16 |
Le mode est 10.
| notes xi | 5 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 16 | Total |
| effectifs ni | 1 | 1 | 4 | 2 | 2 | 4 | 1 | 1 | 1 | 16 |
Cette série est dite série bimodale car on voit apparaître deux modes : 9 et 12.
Dans le cas d'une variable continue, on peut entendre parler de classe modale qui serait la classe de plus grand effectif. Mais il faut se méfier de cette notion car, plus la classe est de grande amplitude, plus son effectif est important sans pour autant que cela soit significatif. Cette notion de classe modale définie par les effectifs de la classe n'a de sens que si les classes ont même amplitude. Si les amplitudes sont différentes, il faut aller chercher sur l'histogramme la classe associée au rectangle de plus grande hauteur.
| Salaires | entre 0 (inclus) et 8 exclus | entre 8 (inclus) et 12 exclus | entre 12 (inclus) et 16 exclus | entre 16 (inclus) et 20 exclus | entre 20 (inclus) et 30 exclus | entre 30 (inclus) et 40 exclus | entre 40 (inclus) et 60 exclus | Total |
| Effectifs | 306 | 231 | 385 | 1180 | 1468 | 568 | 232 | 4370 |
L'observation de ce tableau laisse penser que la classe modale serait la classe [20;30[. Mais une observation de l'histogramme corrige cette idée fausse :
Déciles
Les déciles sont les 9 valeurs qui partagent la population en 10 sous-populations de même taille.
Cas de la variable discrète
On travaillera ici par approximation : le ne décile Dn est la première valeur du caractère tel que l'intervalle [xmin, Dn] regroupe au moins n dixième de la population.
Exemple Série de 30 notes, 9e décile = 27e valeur.
4, 5, 6, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 10, 10,10, 10, 10, 11, 11, 11, 12, 12, 12, 13, 13, 14, 14, 15, 16
D9= 14
Cas de la variable continue
On calcule les déciles comme la médiane et les quartiles, graphiquement grâce au polygone des fréquences cumulées croissantes, et par interpolation linéaire grâce au tableau correspondant.
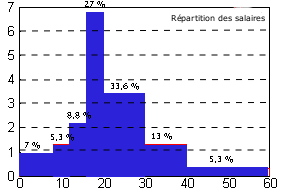
Utilisation du polygone des fréquences cumulées croissantes
Les droites d'équation y = 10, y = 20 ... y = 90 coupent le polygone en des points dont les abscisses valent environ D1=10,5, D2= 15,5...D9=36,5
Utilisation du tableau des fréquences cumulées croissantes
Le tableau des fréquences cumulées croissantes est :
| xi | 0 | 8 | 12 | 16 | 20 | 30 | 40 | 60 |
| fréquences cumulées croissantes | 0 | 7 | 12,3 | 21,1 | 48,1 | 81,7 | 94,7 | 100 |
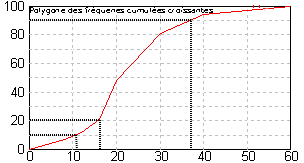
10% est atteint dans l'intervalle [8;12] soit pour une valeur de D1 obtenue par interpolation linéaire
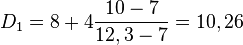
20% est atteint dans l'intervalle [12,16] soit pour une valeur de D2 obtenue par interpolation linéaire
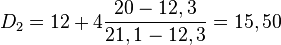
90% est atteint dans l'intervalle [30;40] soit pour une valeur de D9 obtenue par interpolation linéaire