Démonstrations du théorème du minimax - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Cet article ne fait que recenser des preuves du théorème du minimax de John von Neumann. L'énoncé du théorème ainsi qu'une présentation globale de la variété de ses démonstrations sont disponibles dans l'article principal Théorème du minimax de von Neumann auquel on se réfèrera donc.
Toutes les preuves commencent par la même remarque, selon laquelle l'inégalité
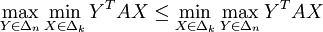
Preuves par arguments de convexité
La preuve de Jean Ville
La preuve qui suit ci-dessous est une variante de celle de Jean Ville et n'utilise que des arguments de convexité élémentaires.
Supposons que l'inégalité entre le maximin et le minimax soit stricte, et introduisons une constante c strictement comprise entre ces deux réels. Si on retranche c à tous les coefficients de A, la quantité YTAX est diminuée de c pour chaque
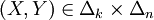
Il nous suffit ainsi de montrer qu'il est impossible que le maximin soit strictement négatif tandis que le minimax est strictement positif.
Dans l'espace des vecteurs-colonnes à n entrées, notons Cj (
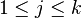
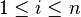
1er cas : si Y1 = 0. Ceci signifie que
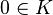
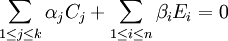
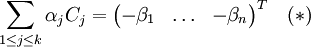
Dans cette égalité il n'est pas possible que tous les αj soient nuls (cela entraînerait la nullité de tous les βi) et cela a donc un sens de considérer le vecteur
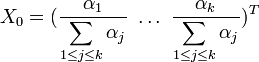
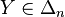
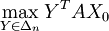
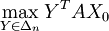
2nd cas : si
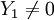
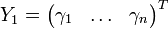
 dont on déduit
dont on déduit
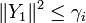
 , on constate que chaque
, on constate que chaque  est un réel strictement positif, et donc que le vecteur
est un réel strictement positif, et donc que le vecteur  est à coefficients strictement positifs. Il n'y a plus qu'à introduire
est à coefficients strictement positifs. Il n'y a plus qu'à introduire
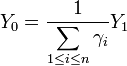
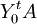
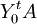
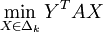
Le théorème du minimax comme corollaire du théorème de dualité en programmation linéaire
On se réfèrera à l'article programmation linéaire pour l'énoncé du théorème et les notations utilisées dans l'écriture des programmes linéaires.
On note e la matrice colonne
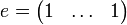
On rappelle qu'en programmation linéaire, pour deux matrices de même taille u et v, on convient de noter
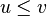
Quitte à augmenter d'une même quantité tous les coefficients de A, on peut supposer le maximin strictement positif. On notera le maximin
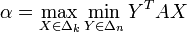
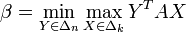
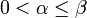
On remarque préalablement (c'est facile) que pour X fixé,
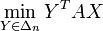
Soit t un réel strictement positif. On peut écrire la suite d'équivalences suivantes :
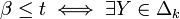
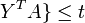
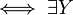
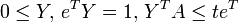
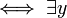
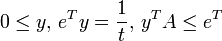
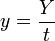
Il apparaît à la suite de ce calcul que le minimax est l'inverse de la valeur du programme linéaire :
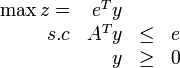
(on utilise ici les notations de l'article programmation linéaire).
Un calcul similaire montre que le maximin est l'inverse de la valeur du programme linéaire :
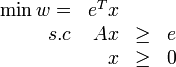
Le théorème de dualité en programmation linéaire garantit donc leur égalité.

















































