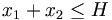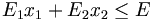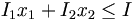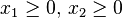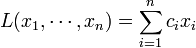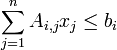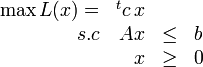Programmation linéaire - Définition

Introduction

En mathématiques, les problèmes de programmation linéaire (PL) sont des problèmes d'optimisation où la fonction objectif et les contraintes sont toutes linéaires. Néanmoins, la plupart des résultats présentés ici sont également vrais si l'objectif est une fonction monotone croissante de chaque variable considérée. La programmation linéaire désigne également la manière de résoudre les problèmes linéaires.

La programmation linéaire est un domaine central de l'optimisation, car les problèmes de PL sont les problèmes d'optimisation les plus faciles - toutes les contraintes y étant linéaires. Beaucoup de problèmes réels de recherche opérationnelle peuvent être exprimés comme un problème de PL. Pour cette raison un grand nombre d'algorithmes pour la résolution d'autres problèmes d'optimisation sont fondés sur la résolution de problèmes linéaires.

Le terme programmation linéaire suppose que les solutions à trouver doivent être représentées en variables réelles. S'il est nécessaire d'utiliser des variables discrètes dans la modélisation du problème (contraintes dites d'intégrité), on parle alors de programmation linéaire en nombres entiers (PLNE). Il est important de savoir que ces derniers sont nettement plus complexes à résoudre que les PL à variables continues.

Exemple

Considérons un agriculteur qui possède des terres, de superficie égale à H hectares, dans lesquelles il peut planter du blé et du maïs. L'agriculteur possède une quantité E d'engrais et I d'insecticide. Le blé nécessite une quantité E₁ d'engrais par hectare et I₁ d'insecticide par hectare. Les quantités correspondantes pour le maïs sont notées E₂ et I₂.

Soit P₁ le prix de vente du blé et P₂ celui du maïs. Si l'on note par x₁ et x₂ le nombre d'hectares à planter en blé et en maïs, alors le nombre optimal d'hectares à planter en blé et en maïs peut être exprimé comme un programme linéaire:

maximiser	P1x1 + P2x2	(maximiser le revenu net)
sous contraintes		(borne sur le nombre total d'hectares)
		(borne sur la quantité d'engrais)
		(borne sur la quantité d'insecticide)
		(on ne peut pas planter un nombre négatif d'hectares)

Dualité

Tous les programmes linéaires peuvent s'écrire sous la forme suivante :

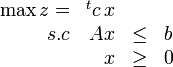
où c et x sont des vecteurs de taille n, b un vecteur de taille m, et A une matrice de taille . Si on désigne cette représentation sous le terme de forme primale, on désigne alors sous le terme de forme duale le problème suivant :

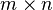
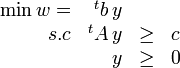
où A, b et c sont les mêmes et y un vecteur de taille m.

Les deux problèmes sont très fortement liés. Si l'un d'entre eux possède une solution optimale, alors l'autre aussi. De plus, les deux solutions ont alors la même valeur (w ^* = z ^* ). Si l'un d'entre eux est non-borné, l'autre ne possède pas de solution.

Outre son intérêt théorique, le problème dual possède de très intéressantes applications économiques. À chaque contrainte primale correspond une variable duale. La valeur de cette variable dans la solution optimale représente le coût marginal associé à la contrainte primale.

Théorie

Comme l'exemple précédent le montre, la programmation consiste à déterminer disons n variables, afin de maximiser l'objectif linéaire

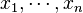
sous différentes contraintes, comme par exemple les m inégalités suivantes

pour i allant de 1 à m. De telles contraintes permettent d'inclure des contraintes de signe, comme par exemple ou . L'adoption de l'écriture matricielle de la forme standard donne

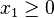
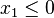
On peut, lors de la programmation linéaire, chercher à minimiser la fonction objectif. On se ramène au cas précédent (la forme standard) en cherchant à maximiser .

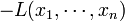
D'un point de vue géométrique, les contraintes linéaires forment un polyèdre convexe (ou polytope). Si la fonction objectif est elle aussi linéaire, tous les optima locaux sont également des optima globaux; cela reste vrai si elle est monotone croissante sur chaque variable considérée, le cas linéaire ne représentant qu'un cas particulier dont la propriété n'est d'ailleurs pas utilisée.

Il y a deux cas où il n'existe pas de solution optimale. Le premier est lorsque les contraintes se contredisent mutuellement (par exemple ). Dans un tel cas, le polytope est vide et il n'y a pas de solution optimale puisqu'il n'y a pas de solution du tout. Le PL est alors infaisable.

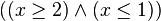
Le polyèdre peut également être non-borné dans la direction définie par la fonction objectif (par exemple x₁ + 3x₂ tel que , , ). Dans ce cas, il n'y a pas de solution optimale puisqu'il est possible de construire des solutions satisfaisant les contraintes avec des valeurs arbitrairement élevées (ou basses) de la fonction objectif.

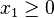
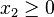
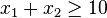
En dehors de ces deux cas (qui sont finalement rares dans les problèmes pratiques), l'optimum est toujours atteint à un sommet du polytope. Cependant, l'optimum n'est pas nécessairement unique : il est possible d'avoir un ensemble de solutions optimales correspondant à une arête ou à une face du polytope, voire au polytope en entier.