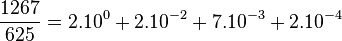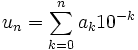Développement décimal - Définition
La liste des auteurs de cet article est disponible ici.
Cas des nombres décimaux
Un nombre décimal est un nombre pouvant s'écrire sous la forme
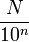
Un nombre décimal positif possède alors un développement décimal limité comportant des puissances de 10 à exposant négatif mais le plus petit exposant ne peut être que - n.
Exemple :
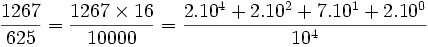
Et on vérifie très simplement à l'aide d'une calculatrice que
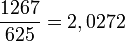
Réciproquement : tout nombre possédant un développement décimal limité est un nombre décimal car il suffit de le multiplier par la puissance de 10 adéquate pour retomber sur un entier.
Régularité dans les développement décimaux illimités
Sauf pour les décimaux et les rationnels dont le développement illimité est périodique, il n'est en général pas possible de « prévoir » les décimales d'un réel. Seuls des calculs poussés permettent de découvrir les premières décimales (on connaît jusqu'à présent les 1 241 100 000 000 premières décimales de π.)
Des études portant sur la fréquence des entiers dans les développement décimaux de
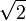
Lorsque la fréquence d'apparition de chaque chiffre est de 10% dans le développement décimal, et plus généralement que la fréquence d'apparition d'un suite de n chiffres donnée est (pour chaque suite) de 10-n, on dit que le réel est un nombre normal.
Cas des nombres réels
Si x est un nombre réel, on construit les suites de nombres décimaux suivantes :
-
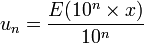
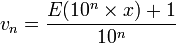
un s'appelle l'approximation décimale de x par défaut à 10-n et vn celle par excès.
On démontre facilement que un et un+1 ne diffèrent (éventuellement) que sur la n+1e décimale qui est de 0 pour un et de an+1 pour un+1.
un s'écrit alors
où a0 est un entier relatif et où tous les ak pour k = 1 à n sont des entiers compris dans {0, …, 9}.
On démontre aussi que (un) et (vn) sont des suites adjacentes encadrant x donc elles convergent vers x. On appelle alors développement décimal illimité la suite (an) et on remarquera que
-
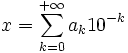
Réciproquement, si (an) est une suite d'entiers tels que tous les ak pour k = 1 à n sont des entiers compris dans {0, …, 9}, on démontre que la série
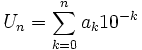
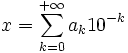
- Si la suite (an) converge vers 9 (tous les termes égaux à 9 à partir d'un certain rang k). Alors x est un décimal d'ordre k - 1. La suite (un) définie dans la première partie ne coincidera pas à la suite (Un). La suite (an) ne sera pas appelée un DDI.
- Si la suite ne converge pas vers 9, la suite (un) définie dans la première partie coincidera à la suite (Un) . La suite (an) sera appelée un DDI.
Cette construction d'un développement illimité permet de retrouver le développement d'un décimal 3,5670000…, d'un rationnel 3,25743743743… non impropre.
On démontre que cette définition construit une bijection entre les réels et les suites (an) d'entiers tels que tous les ak pour k = 1 à n sont des entiers compris dans {0, …, 9} ne convergeant pas vers 9.
Développement en base quelconque
Utiliser un développement décimal fait jouer un rôle particulier à la base 10. Tout ce qui précède s'applique à n'importe quel nombre entier b (comme base), supérieur à 1. Cette fois, les nombres admettant deux développements seront ceux de la forme
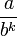
En fait la base 10 présente surtout un intérêt pratique, c'est celle à laquelle nous sommes habitués. Les bases 2 et 3 notamment sont très intéressantes. Plaçons nous en base 2. L'application de
![d:\{0,1\}^\N \rightarrow [0,1]](https://static.techno-science.net/illustration/Definitions/autres/d/d647a8a70831a9fe1efc9121f40efc6c_f5e073c01b149b6627a2679f711d7e39.png)
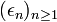
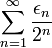
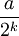
Plaçons nous maintenant en base 3. L'application qui à la même suite
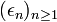
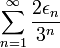
![[0,1]\,](https://static.techno-science.net/illustration/Definitions/autres/d/d09694b77d8a3a03f6879fa37f09d0b0_c0411dcdc7776b6e09605dc7ec8741eb.png)
![[0,1]\times[0,1]\,](https://static.techno-science.net/illustration/Definitions/autres/7/709ba53bd4deaad714fb66ca0a272758_090d3ceb01660d1bfe72f925519ebc5e.png)