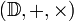Nombre décimal - Définition

Introduction

Un nombre décimal est un nombre possédant un développement décimal limité et pouvant s'écrire sous la forme (où a et p sont des entiers relatifs). Ce n'est pas le cas, par exemple, du nombre qui possède cependant autant d'approximations décimales que l'on veut :

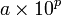
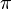
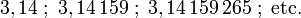
Caractérisation

Si a est un nombre rationnel, les propriétés suivantes sont équivalentes et caractérisent le fait que le nombre a est décimal :

• a admet un développement décimal limité (c'est-à-dire avec un nombre fini de chiffres différents de 0).
• Il existe et tels que : .
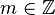
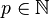
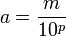
• La fraction irréductible de a est de la forme , où b est un entier relatif et m et p des entiers naturels.
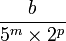
• a possède deux développements décimaux distincts.

Remarques

• La première assertion prouve que 1,6666 est un nombre décimal et que 1,6666... (qui s'écrirait avec une infinité de 6) n'en est pas un.
• La deuxième assertion nous dit que est un nombre décimal, mais elle ne peut pas être utilisée pour prouver qu'un nombre n'est pas décimal.
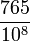
• La troisième assertion nous donne une méthode pour reconnaître si un nombre rationnel est décimal : il suffit de déterminer sa fraction irréductible (par exemple en calculant le PGCD de son numérateur et de son dénominateur), puis de tester si le dénominateur est uniquement divisible par 2 et 5.
• La quatrième assertion fait souvent figure de « curiosité ». Le nombre 2,5 peut aussi être écrit 2,4999... (avec une infinité de 9). Pour des détails, voir l'article Développement décimal de l'unité.

Topologie

est dense dans . Autrement dit, tout nombre réel est la limite d'une suite de nombres décimaux. Ce théorème est fréquemment utilisé lors de la recherche de valeurs approchées.

Structure algébrique

L'ensemble des décimaux est souvent noté . est un anneau intègre commutatif. Son corps des fractions étant .