Nombre normal - Définition

En mathématiques, un nombre normal est un nombre réel qui a ses chiffres équidistribués dans son développement décimal.

Supposons B un ensemble fini de cardinal b>1 et x un nombre réel. Si s est une suite finie de chiffres en base B, nous écrivons N(s,n) pour le nombre d'apparitions de la suite s parmi les n premiers chiffres de x. Le nombre x est appelé normal en base B si

Le nombre x est dit nombre normal (ou quelquefois nombre absolument normal) s'il est normal dans toute base.

Le concept fut introduit par le mathématicien français Émile Borel en 1909. En utilisant le lemme de Borel-Cantelli, il démontra le théorème du nombre normal: presque tous les nombres réels sont normaux, dans le sens où l'ensemble des nombres non-normaux est de mesure nulle (pour la mesure de Lebesgue). Ce théorème établit l'existence des nombres normaux, mais Waclaw Sierpinski fut le premier à donner un exemple de l'un d'eux.

L'ensemble des nombres non-normaux n'est pas dénombrable. En effet, il y a une quantité indénombrable de réels qui ne contiennent pas le chiffre 5 dans leur expansion décimale, et aucun de ceux-ci n'est normal.

Le nombre de Champernowne

0,1234567891011121314151617...

qui contient dans son développement décimal la concaténation de tous les nombres naturels est normal en base 10, mais il ne l'est pas dans certaines autres bases.

La constante de Copeland-Erdős

0,2357111317192329313741...

obtenue en concatenant les nombres premiers est connue comme étant un nombre normal en base 10.

Aucun nombre rationnel n'est normal dans aucune base, puisque la suite de chiffres dans le développement des nombres rationnels est périodique à partir d'un certain rang. Waclaw Sierpinski a fourni la première construction explicite d'un nombre normal en 1917. Un nombre normal calculable fut construit par Verónica Becher et Santiago Figueira ; un exemple de nombre normal non-calculable est donné par la constante de Chaitin .

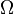
Il est extrêmement difficile de démontrer la normalité de nombres pourtant simples. Par exemple, on ne sait pas si √2, , ln(2) ou e sont normaux (mais tous sont conjecturés comme normaux, conformément aux expériences). Nous ne savons même pas quels chiffres apparaissent infiniment souvent dans le développement décimal de ces constantes. David H. Bailey et Richard E. Crandall ont conjecturé en 2001 que tout nombre algébrique irrationnel est normal ; bien qu'aucun contre-exemple ne soit connu, on ne connait pas non plus de nombre algébrique qui soit normal dans une base.