Anneau noethérien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

En mathématique, un anneau noethérien est un cas particulier d'anneau, c'est-à-dire d'un ensemble muni d'une addition et d'une multiplication compatible avec l'addition, au sens de la distributivité.
De nombreuses questions mathématiques s'expriment dans un contexte d'anneau, les endomorphismes d'un espace vectoriel ou d'un module sur un anneau, les entiers algébriques de la théorie algébrique des nombres, ou encore les surfaces de la géométrie algébrique. Si les anneaux sont nombreux, rares sont ceux disposant des propriétés communes aux exemples les plus simples comme les entiers relatifs ou les polynômes à coefficients dans un corps. La division euclidienne n'existe en général plus, les idéaux, outils majeurs de la théorie des anneaux, ne sont plus toujours principaux et le théorème fondamental de l'arithmétique ne possède plus d'équivalent.
L'approche consistant à étudier une question uniquement sous l'angle des propriétés spécifiques d'une structure d'anneau particulière s'est révélée fructueuse. Richard Dedekind l'a utilisée avec succès en arithmétique et David Hilbert en géométrie algébrique. Emmy Noether choisit un nombre plus limité de propriétés vérifiées par certains anneaux et démontre de nombreux résultats sur ceux-ci.
Le terme d'anneau noethérien apparait en 1954 sous la plume de mathématiciens japonais.
Approche intuitive
Dans certains cas simples, tous les idéaux d'un anneau A sont principaux. Si A est considéré comme un module sur lui-même, ses idéaux sont alors des sous-modules engendrés par un élément. Cette situation n'est cependant pas générale.
En arithmétique, il est fréquent d'utiliser des anneaux d'entiers algébriques comme par exemple les entiers quadratiques de la forme a + b.i√5 où a et b sont des entiers relatifs et i l'unité imaginaire complexe. Il existe en effet dans cet anneau un idéal, formé des éléments de la forme 2.a + b(1 + i√5), où a et b sont des entiers relatifs, qui n'est pas principal, c'est-à-dire n'est pas engendré par un unique élément. En revanche, il est engendré par un nombre fini d'éléments, ici deux. Dans l'anneau considéré, c'est-à-dire Z[i.√5] (la lettre Z désigne dans tout l'article l'anneau des entiers relatifs) tous les idéaux sont engendrés par un ou deux éléments. Cette configuration est la même pour tout anneau d'entiers algébriques d'une extension finie du corps des nombres rationnels.
Cette configuration se retrouve en théorie des groupes. Si G est un groupe abélien de type fini (c'est-à-dire admettant une famille génératrice finie) muni de sa structure canonique de Z-module, tout sous-groupe de G, qui est aussi un sous-module, admet une famille génératrice finie. La propriété est la même, même si elle s'applique à un module et non plus à un anneau.
Cette propriété, indiquant que tout idéal d'un anneau A admet une famille génératrice finie si l'idéal est considéré comme un sous A-module, est fréquente en mathématiques. Elle correspond à la notion formalisée par la définition d'anneau noethérien. La notion de module noethérien est un substitut de l'hypothèse de la dimension finie en algèbre linéaire.
Propriétés
Tout sous-module et tout module quotient d'un module noethérien sont noethériens, et l'équivalence suivante donne une réciproque :
- Soit P un sous-module de M, le module M est noethérien si et seulement si P et M / P le sont.
- Si le module M est noethérien, tout sous-module P l'est aussi :
En effet, tout sous-module de P est un sous-module de M donc est de type fini.
- Si le module M est noethérien, tout module quotient M / P l'est aussi :
Soient Q un sous-module du quotient M / P, et R l'image réciproque de Q par la projection canonique de M dans M / P. Alors R est un sous-module de M donc possède une famille génératrice finie. L'image de cette famille par la projection canonique engendre Q, ce qui montre que le quotient est aussi noethérien.
- Si le sous-module P et le module quotient M / P sont noethériens alors le module M l'est aussi :
Soient R un sous-module de M, F une famille finie engendrant R∩P et G une famille finie engendrant l'image de R par la projection canonique de M dans M / P. Choisissons une famille finie H de vecteurs de R dont les projetés soient les éléments de G. Alors R est engendré par la famille finie
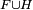
On en déduit aussitôt :
- tout anneau quotient (par un idéal bilatère) d'un anneau noethérien à gauche est noethérien à gauche et
- si A est un anneau noethérien, les A-modules noethériens sont exactement les A-modules de type fini.
La décomposition des idéaux est plus délicate. Dans l'anneau commutatif principal Z par exemple, l'idéal 12Z est égal à la fois au produit des idéaux 2Z, 2Z et 3Z, et à l'intersection des idéaux 22Z et 3Z (qui est aussi leur produit). Dans un anneau commutatif seulement noethérien, trois propriétés s'en rapprochent (la première est utilisée dans l'article Anneau de valuation discrète, la deuxième est le théorème de Lasker-Noether) :
Soit A un anneau commutatif noethérien.
- Tout idéal de A contient un produit d'idéaux premiers, ou plus précisément, tout idéal I de A contient un produit d'idéaux premiers qui contiennent I.
- Pour tout idéal de A, il existe un nombre fini d'idéaux premiers minimaux contenant cet idéal.
- Tout idéal radiciel de A est intersection finie d'idéaux premiers.
- Tout idéal de A est décomposable, c'est-à-dire intersection finie d'idéaux primaires.
- Si A est intègre, tout élément non nul et non inversible est produit d'un nombre fini d'éléments irréductibles.
- Tout idéal de A contient un produit d'idéaux premiers, ou plus précisément, tout idéal I de A contient un produit d'idéaux premiers qui contiennent I :
Montrons la première assertion, par l'absurde. Soit F l'ensemble, supposé non vide, des idéaux de A qui ne contiennent aucun produit d'idéaux premiers (en particulier aucun produit indexé par un singleton, donc les éléments de F ne sont pas premiers, et aucun produit indexé par le vide, donc A n'appartient pas à F). Soit I un élément maximal de F. L'idéal I est propre et non premier. D'après une propriété caractéristique des idéaux non premiers, il existe donc deux idéaux J et K tels que I contienne le produit J.K mais soit strictement contenu dans J et K. Alors (par maximalité de I) les idéaux J et K n'appartiennent pas à F, donc chacun d'eux contient un produit d'idéaux premiers. Comme I contient leur produit, on aboutit à une contradiction, ce qui termine la démonstration du premier point. En raison de la correspondance biunivoque entre les idéaux premiers de l'anneau quotient A/I et ceux de l'anneau A contenant I, on déduit le second point du premier appliqué à l'idéal (0) de l'anneau A/I.
Une preuve plus compliquée, mais instructive, est d'utiliser la décomposition primaire (énoncée dessous), en remarquant que le radical de tout idéal primaire est premier, et que dans un anneau noethérien, tout idéal contient une puissance de son radical.
- Existence et finitude des idéaux premiers minimaux contenant un idéal I :
On sait qu'il existe des idéaux premiers
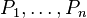
- Tout idéal radiciel de A est intersection finie d'idéaux premiers :
Soit I un idéal radiciel de A. On sait qu'il existe des idéaux premiers
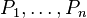
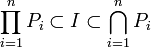
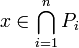
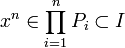
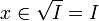
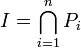
- Tout idéal est intersection finie d'idéaux primaires :
On montre en fait un peu mieux : dans un anneau noethérien, tout idéal est intersection finie d'idéaux irréductibles, et tout idéal irréductible est primaire.
-
- Pour le premier point, on raisonne par l'absurde comme précédemment : soient F l'ensemble, supposé non vide, des idéaux de A qui ne sont pas intersection finie d'irréductibles, et I un élément maximal de F. Alors I est réductible donc égal à l'intersection de deux idéaux J et K dans lesquels il est strictement inclus. Par maximalité, J et K n'appartiennent pas à F, donc chacun d'eux est intersection finie d'irréductibles, d'où la contradiction.
- Pour le second point, cf Le défi algébrique, tome 2, de Claude Mutafian, p. 239, ou Bourbaki, Algèbre commutative, chapitre II, § 2, exercice 22, ou encore Zariski et Samuel, Commutative algebra, vol. 1, p. 209.
(On pourra aussi consulter l'article Décomposition primaire (en), qui étend ce théorème aux modules de type fini sur un anneau noethérien, et la plupart des ouvrages de référence, comme Algebra de S. Lang ou Algèbre commutative chapitre IV de Bourbaki, qui généralisent cela aux modules noethériens sur un anneau commutatif quelconque.)
- Si A est intègre, tout élément non nul et non inversible est produit d'un nombre fini d'irréductibles :
On raisonne à nouveau par l'absurde comme précédemment, en considérant l'ensemble, supposé non vide, des idéaux principaux de A engendrés par des éléments non nuls et non inversibles qui ne vérifient pas la propriété énoncée. Cet ensemble admettant un élément maximal pour l'inclusion, on conclut aisément à une contradiction en étudiant cet élément maximal.