Dual d'un polyèdre - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie, il existe plusieurs façons (géométrique, combinatoire) de mettre les polyèdres en dualité. Dans chaque cas, à tout polyèdre est associé un polyèdre appelé dual du premier, de telle sorte que
- le dual du polyèdre dual est le polyèdre initial,
- les faces de l'un sont en correspondance avec les sommets de l'autre, en respectant les propriétés d'adjacence.
L'exemple le plus simple de dualité s'obtient pour les polyèdres réguliers, en reliant les centres de faces adjacentes. Plus généralement, on définit une dualité en considérant l'opération de conjugaison par rapport à la sphère circonscrite.
On peut se passer de support géométrique et définir une notion de dualité en termes purement combinatoires, qui s'étend d'ailleurs aux polyèdres et polytopes abstraits.
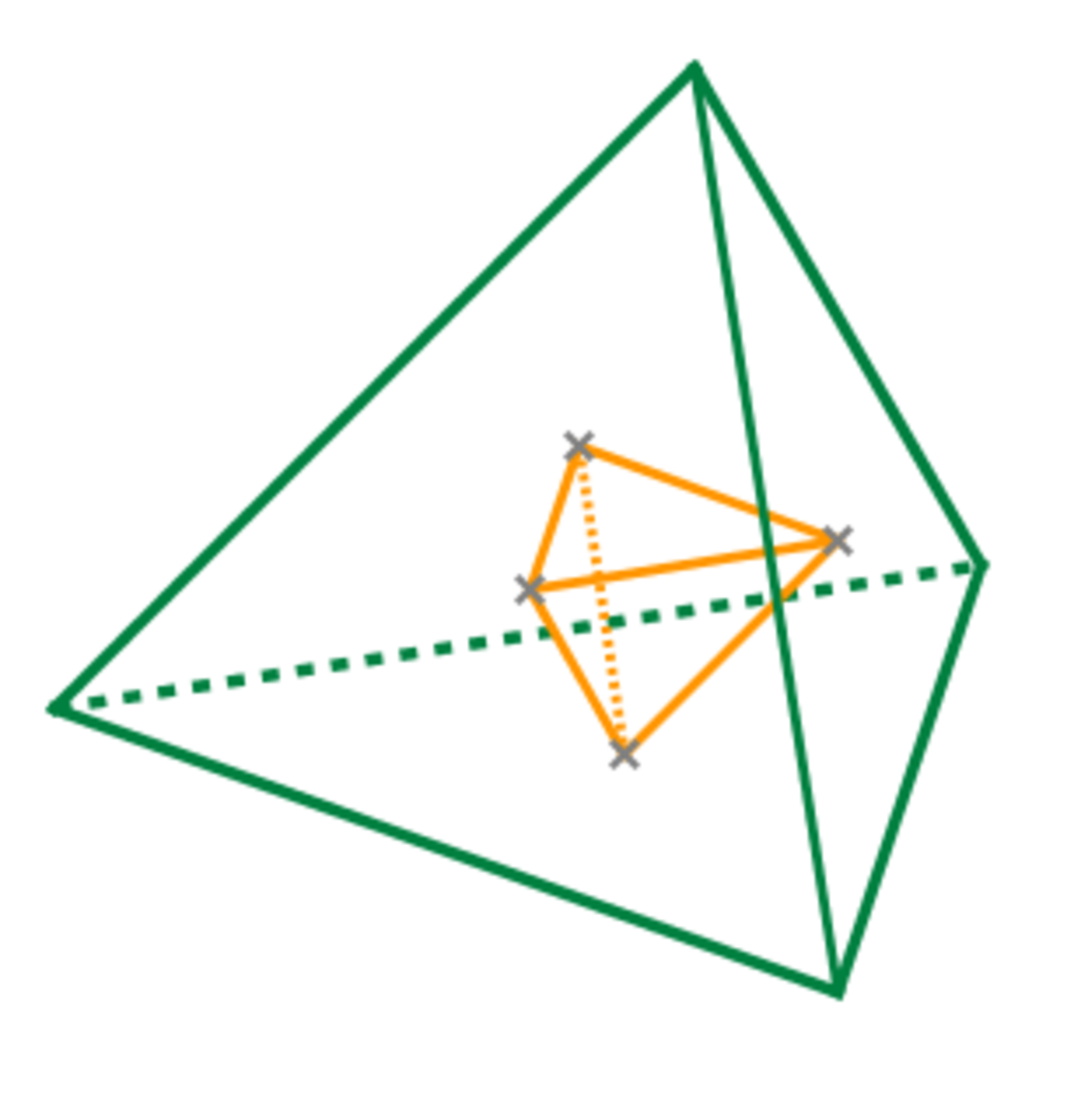
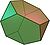
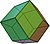
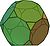
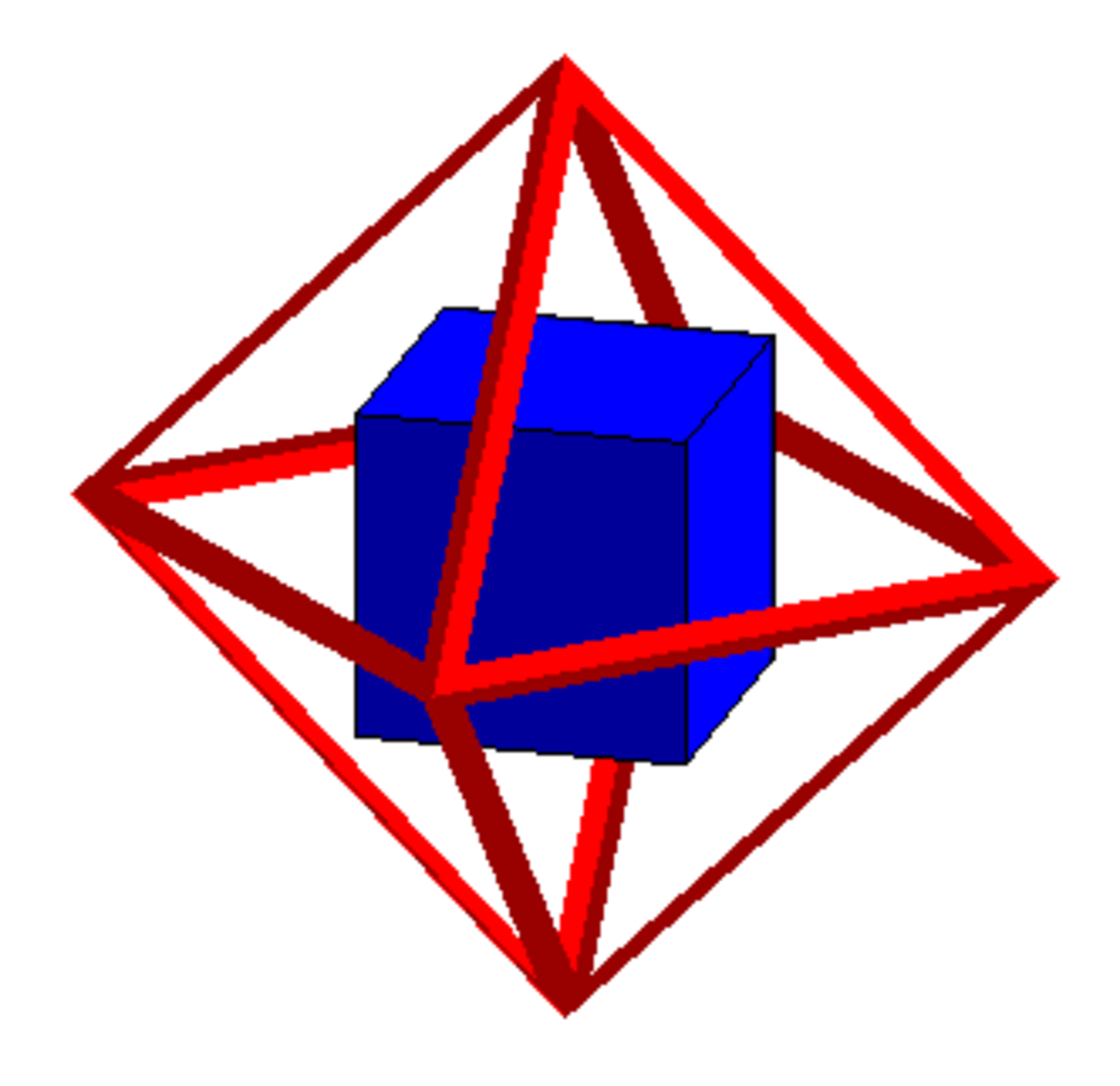
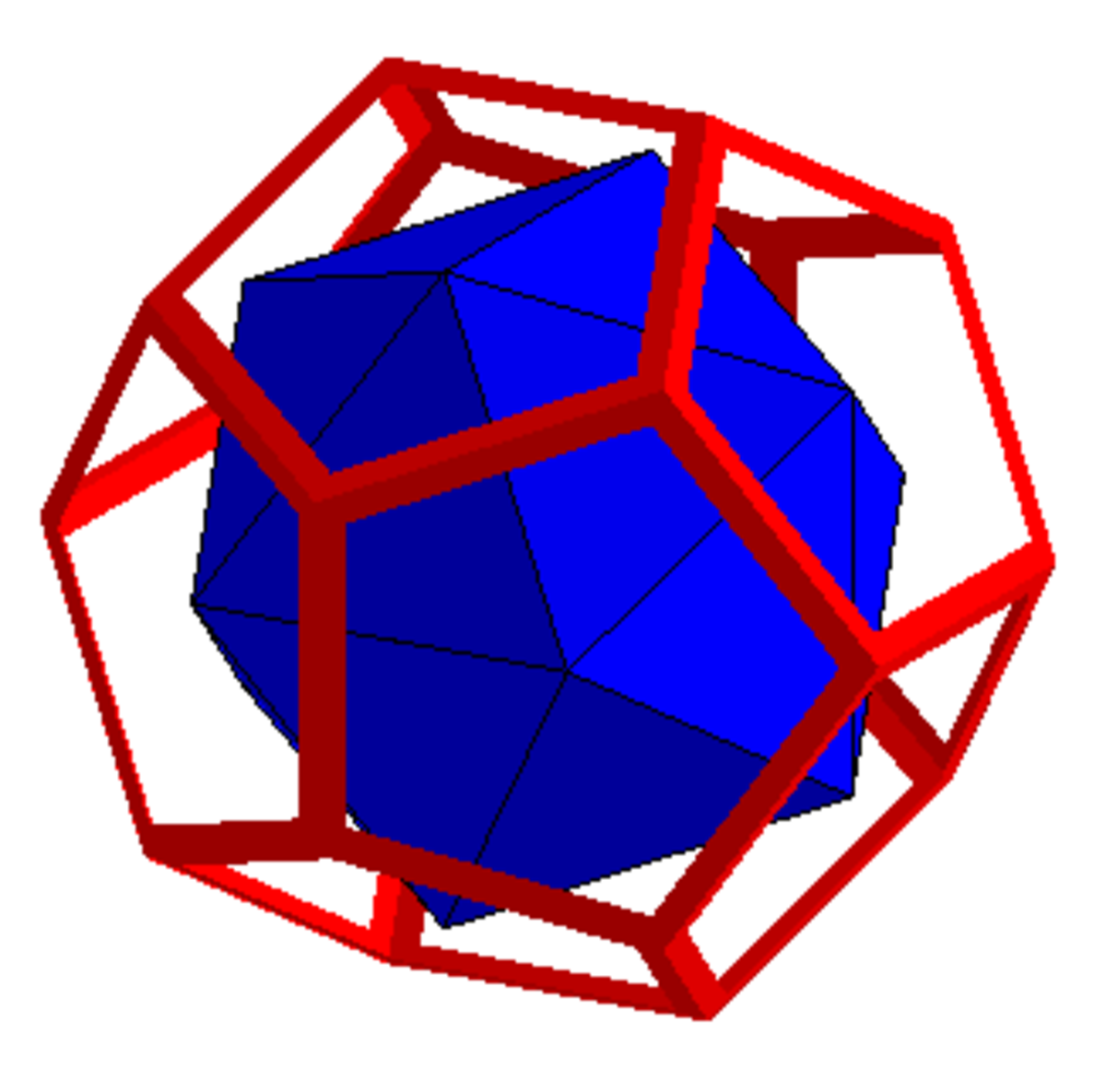
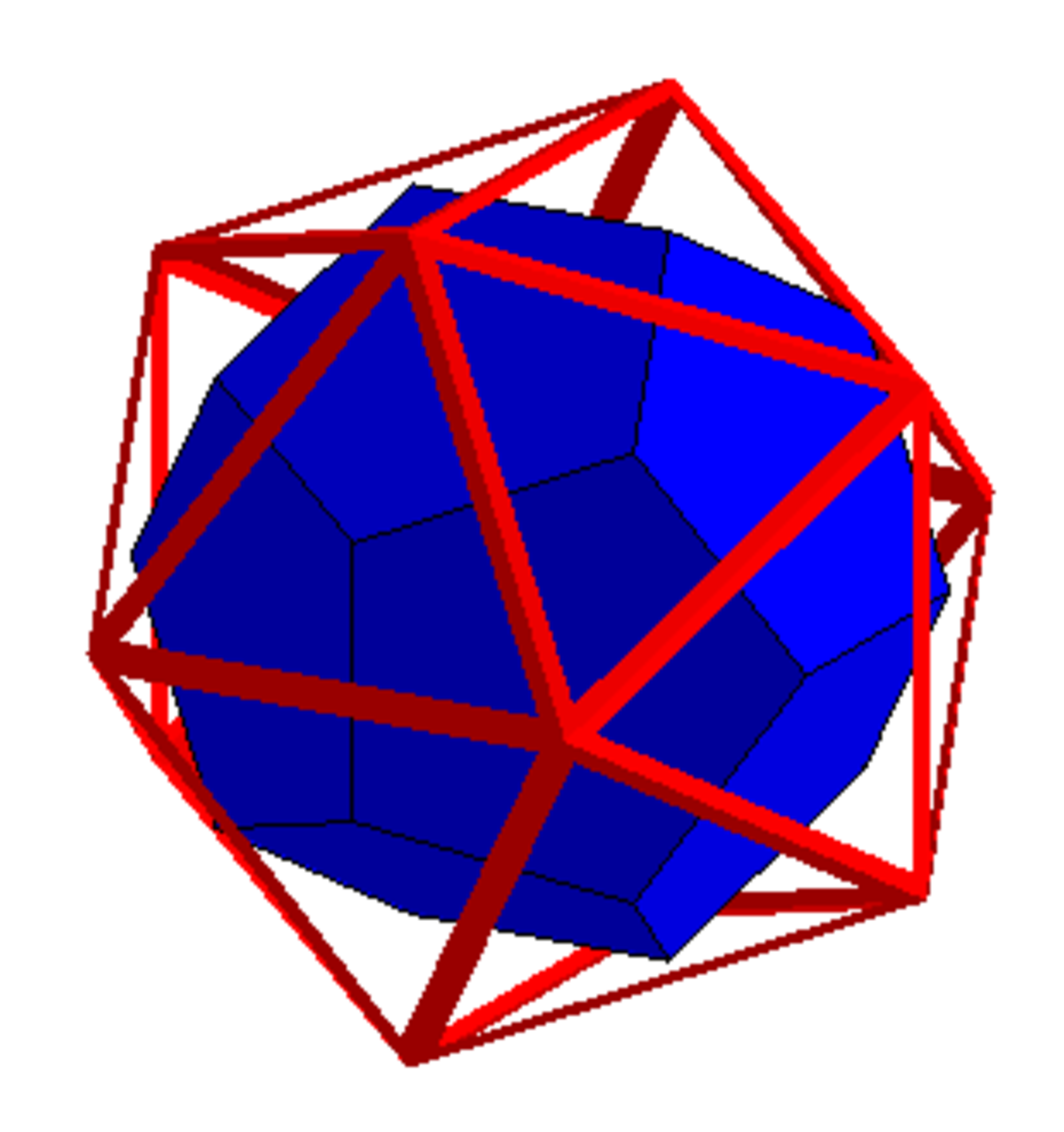
Le cube donne l'octaèdre, le dodécaèdre l'icosaèdre et le tétraèdre est son propre dual.
Le petit dodécaèdre étoilé est le dual du grand dodécaèdre, et le grand dodécaèdre étoilé celui du grand icosaèdre.
Les duaux des solides archimédiens sont les solides de Catalan.
Les duaux des prismes sont des diamants (ou bipyramides), ceux des antiprismes des antidiamants.
| solide | dual | ||
|---|---|---|---|
| tétraèdre |
| tétraèdre |
|
| cube |

| octaèdre |

|
| octaèdre |

| cube |

|
| icosaèdre |
| dodécaèdre | |
| dodécaèdre | icosaèdre |
| |
| petit dodécaèdre étoilé |

| grand dodécaèdre |

|
| grand dodécaèdre étoilé |
| grand icosaèdre |

|
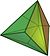
| tétraèdre tronqué |
| triakitétraèdre |
|
| cube tronqué |
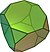
| triakioctaèdre |
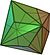
|
| octaèdre tronqué |
| tétrakihexaèdre |
|
| cuboctaèdre |

| dodécaèdre rhombique |
|
| petit rhombicuboctaèdre |

| icositétraèdre trapézoïdal |

|
| grand rhombicuboctaèdre |

| hexakioctaèdre |

|
| cube adouci |
| icositétraèdre pentagonal |
|
| dodécaèdre tronqué |
| triaki-icosaèdre |

|
| icosaèdre tronqué |

| pentakidodécaèdre |

|
| icosidodécaèdre |

| triacontaèdre rhombique |

|
| petit rhombicosidodécaèdre |

| hexacontaèdre trapézoïdal |
|
| grand rhombicosidodécaèdre |

| hexaki icosaèdre |

|
| dodécaèdre adouci |

| hexacontaèdre pentagonal |

|
| géode par triangulation |

| géode en nid d'abeille |

|
Dualité des solides de Platon
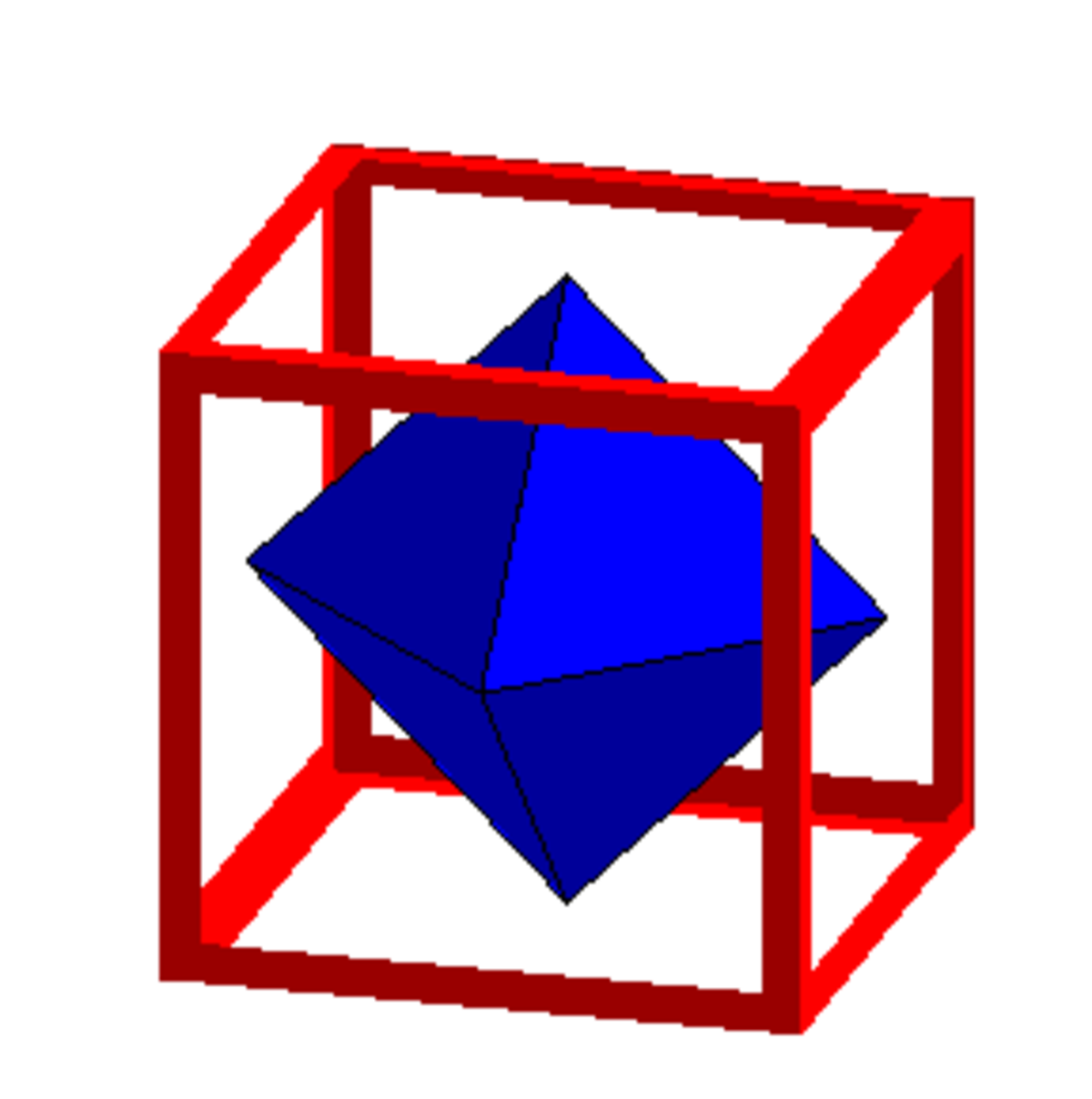
|
|
| Le dual du cube est l'octaèdre | Le dual de l'octaèdre est le cube |
|
|
| Le dual du dodécaèdre est l'icosaèdre | Le dual de l'icosaèdre est le dodécaèdre |