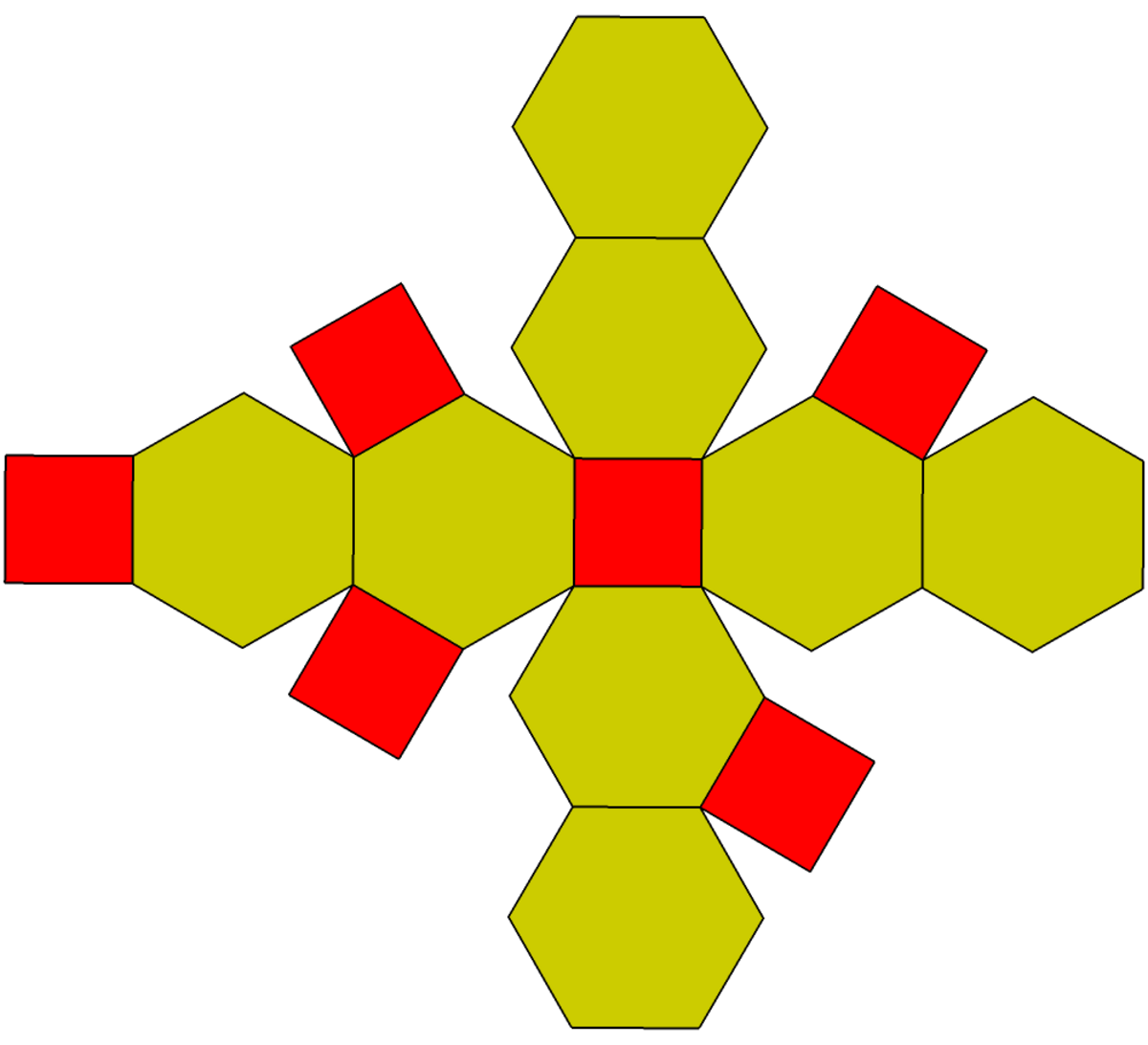
Octaèdre tronqué - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
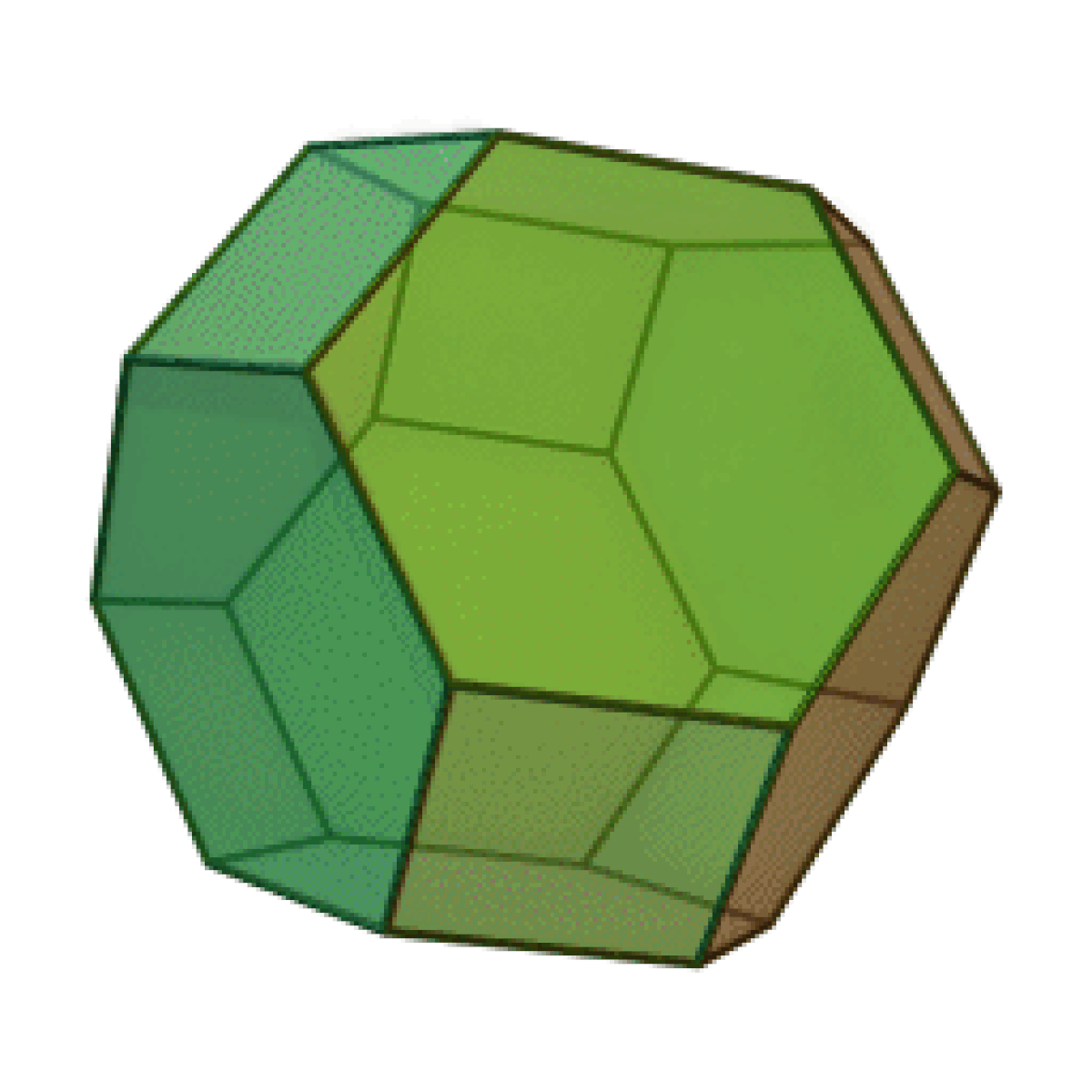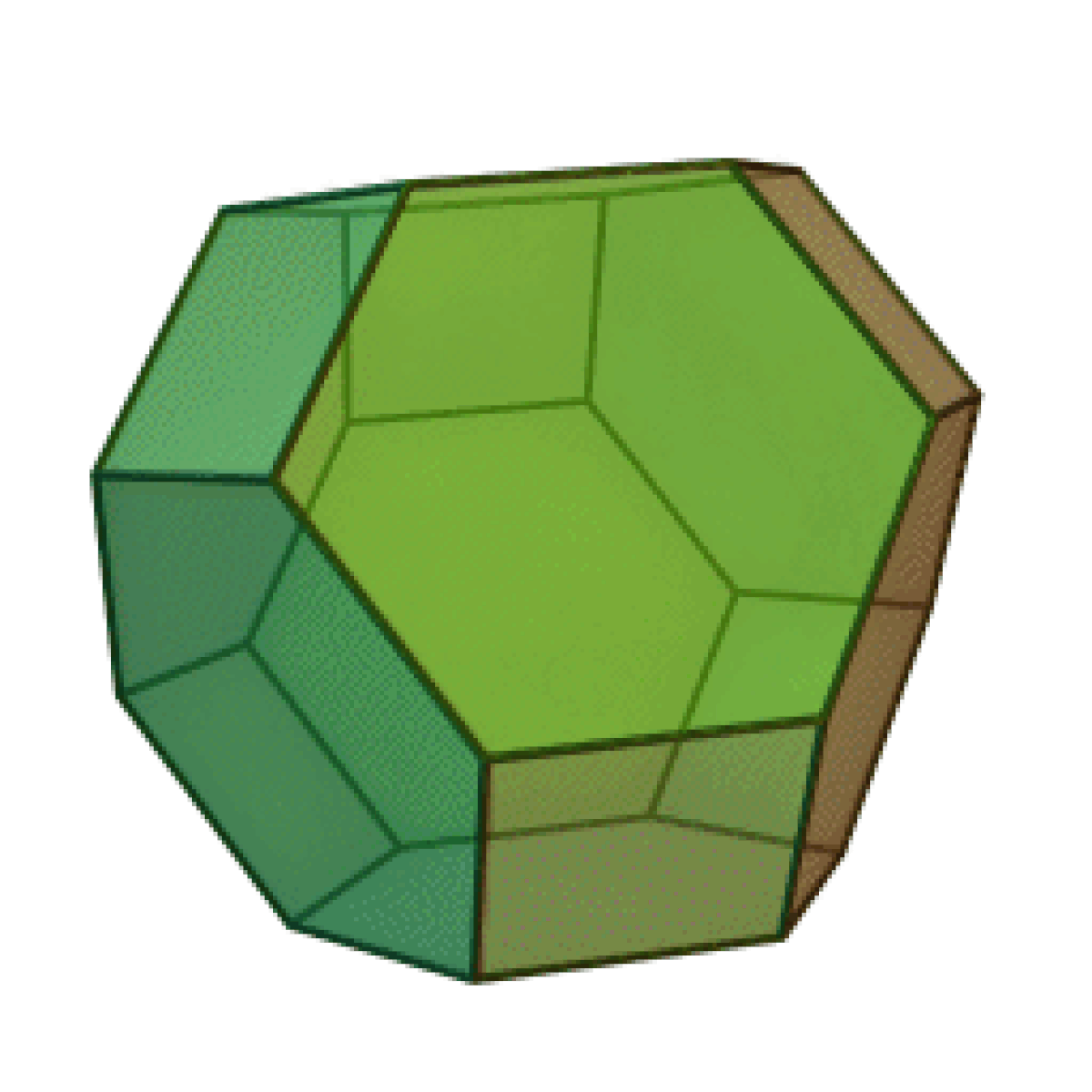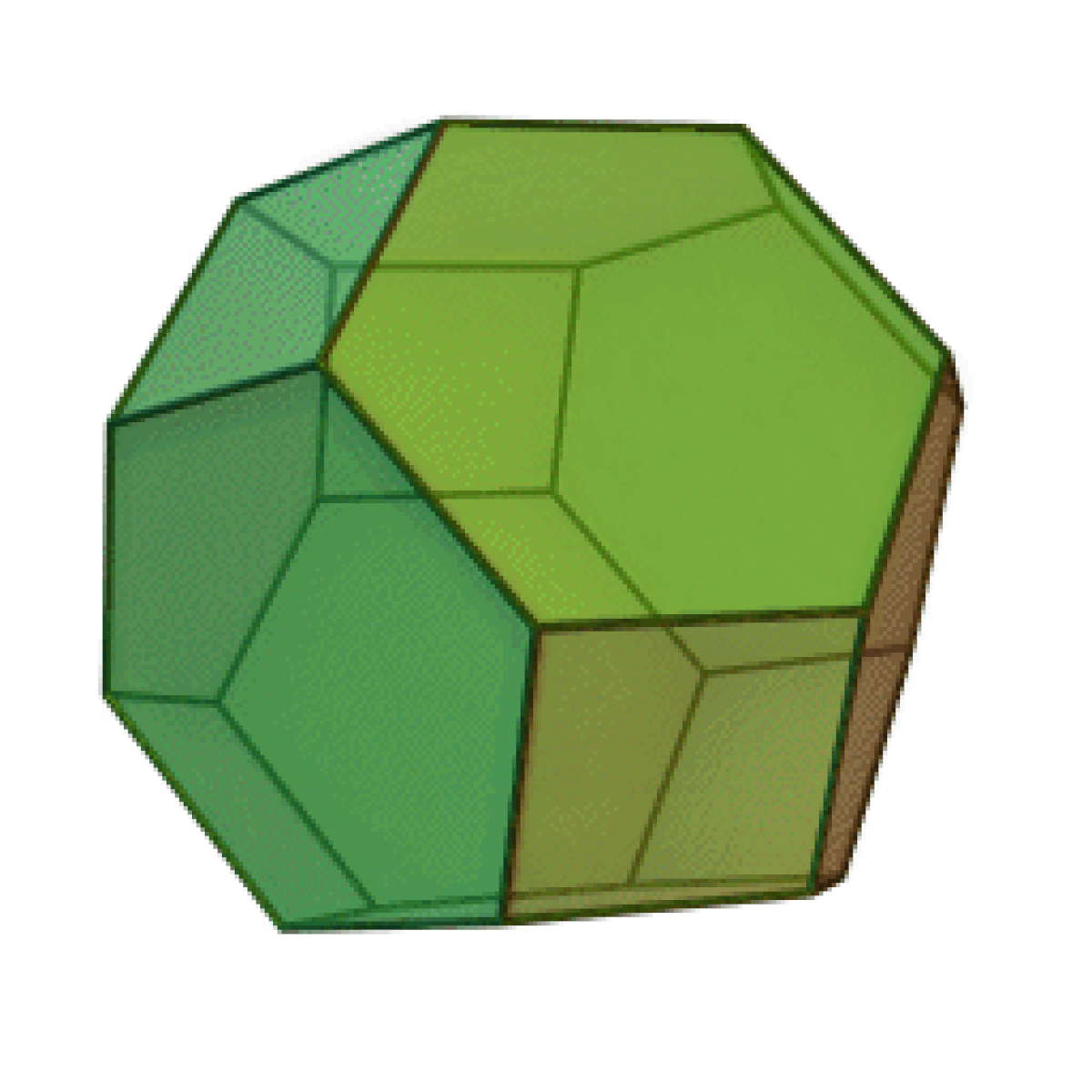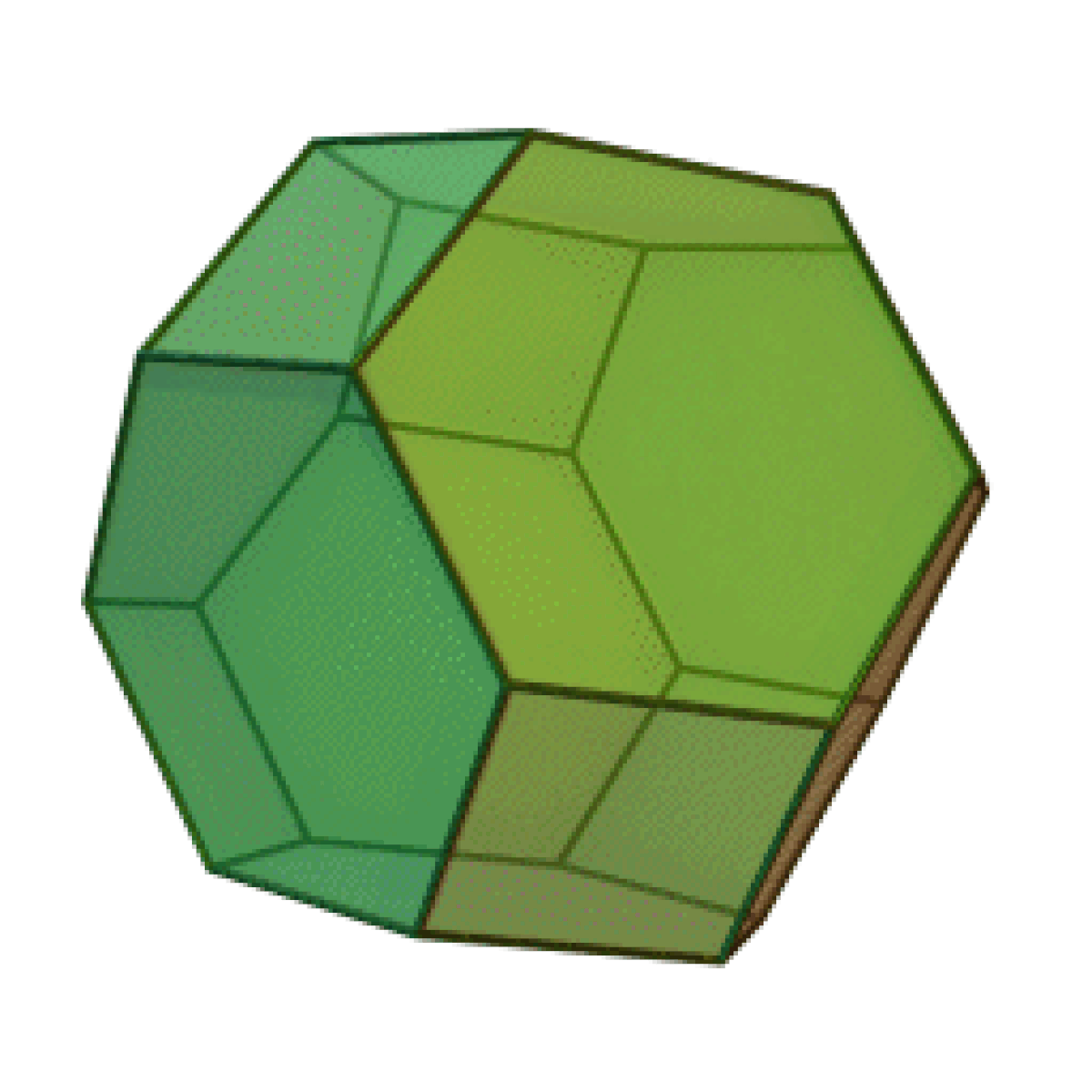
| Octaèdre tronqué | |
|---|---|
 | |
| | |
| Type | Solide d'Archimède |
| Faces | Carrés et hexagones |
| Éléments : · Faces · Arêtes · Sommets · Caractéristique | 14 36 24 2 |
| Faces par sommet | 3 |
| Sommets par face | 4 et 6 |
| Isométries | |
| Dual | Tétrakihexaèdre |
| Propriétés | Semi-régulier et convexe, zonoèdre |
| modifier | |
L'octaèdre tronqué est un solide d'Archimède. Il possède 8 faces hexagonales régulières, 6 faces carrés régulières, 24 sommets et 36 arêtes. Puisque chacune de ses faces possède un centre de symétrie (ou une symétrie à 180°), l'octaèdre tronqué est un zonoèdre.
Coordonnées et permutations
Toutes les permutations de (0, ±1, ±2) sont des coordonnées cartésiennes des sommets d'un octaèdre tronqué centré à l'origine. Les sommets sont aussi les coins de 12 rectangles dont les longueurs sont parallèles aux axes de coordonnées.
L'octaèdre tronqué peut aussi être représenté par plus de coordonnées symétriques en quatre dimensions : toutes les permutations de (1,2,3,4) forment les sommets d'un octaèdre tronqué dans le sous-espace à trois dimensions x+y+z+w=10. Pour cette raison, l'octaèdre tronqué est aussi connu quelquefois sous le nom permutoèdre. La construction se généralise à n quelconque, et forme un polytope à (n-1) dimensions, ses sommets représentent les permutations d'un ensemble de n articles; par exemple, les six permutations de (1,2,3) forment un hexagone régulier dans le plan x+y+z=6.
Mesures et volume
Si son arête est de longueur "a",
- Son volume vaut :
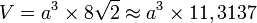
- Sa surface est de :
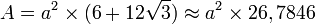
Relations géométriques

Les octaèdres tronqués sont capables de paver un espace à 3 dimensions, en formant un nid d'abeille uniforme convexe. Ce pavage peut aussi être vu comme le pavage de Voronoï du réseau cubique centré.