Dodécaèdre adouci - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Dodécaèdre adouci | |
|---|---|
  | |
| | |
| Type | Solide d'Archimède |
| Faces | Triangles et Pentagones |
| Éléments : · Faces · Arêtes · Sommets · Caractéristique | 92 150 60 2 |
| Faces par sommet | 5 |
| Sommets par face | 3 et 5 |
| Isométries | Ih |
| Dual | Hexacontaèdre pentagonal |
| Propriétés | Semi-régulier et convexe, chiral |
| modifier | |
Le dodécaèdre adouci ou icosidodécaèdre adouci est un solide d'Archimède.
Le dodécaèdre possède 92 faces dont 12 sont des pentagones et les 80 autres sont des triangles équilatéraux. Il possède aussi 150 arêtes et 60 sommets. Il a deux formes distinctes, qui sont les images dans un miroir (ou "énantiomorphes") l'une de l'autre.
Relations géométriques
Le dodécaèdre peut être engendré en prenant les douze faces pentagonales du dodécaèdre, en les tirant de telle façon qu'aucune ne se touchent, puis en leur donnant toutes une petite rotation de leurs centres (toutes en sens horaire (Sh) ou toutes en sens anti-horaire (Sah)) jusqu'à ce que l'espace entre elles puisse être rempli par des triangles équilatéraux.
Coordonnées cartésiennes
Les coordonnées cartésiennes pour les sommets d'un dodécaèdre adouci sont toutes les permutations paires de
-
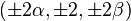
-
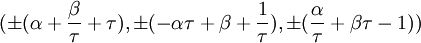
-
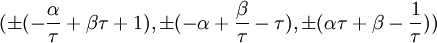
-
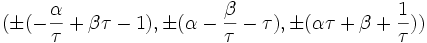
-
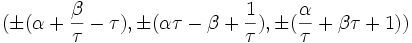
avec un nombre pair de signes plus, où
et
-
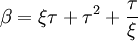
où
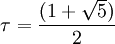
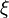
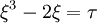
ou approximativement 1,7155615. En prenant les permutations impaires des coordonnées ci-dessus avec un nombre impair de signes plus donne une autre forme, l'énantiomorphe de celle-ci.
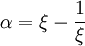
![\xi = \sqrt[3]{\frac{\tau}{2} + \frac{1}{2}\sqrt{\tau - \frac{5}{27}}} + \sqrt[3]{\frac{\tau}{2} - \frac{1}{2}\sqrt{\tau - \frac{5}{27}}}](https://static.techno-science.net/illustration/Definitions/autres/1/159967f20c2df3f26365ea3651cfee6d_6b6e0f8f3027914f839058953ef76e57.png)


















































