Effet Sagnac - Définition

L'addition des vitesses

Les formules précédentes donnent l'addition des vitesses avec la lumière. Mais qu'en est-il de l'addition des vitesses en général. Que vaut l'addition des vitesses sur la circonférence du disque ?

Soit deux observateurs O' et O" se déplaçant à V' et V''.

Un rayon lumineux se déplaçant dans le même sens à pour vitesse respectivement pour O' et O" :

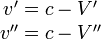
Soit V''' la vitesse relative de O' et O". Un raisonnement identique à celui utilisé dans la présentation de l'effet Sagnac (en utilisant O" comme « signal » pour O et O') montre que

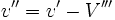
Donc

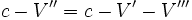
C'est-à-dire

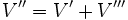
La lumière obéit dans le repère en rotation à l'addition galiléenne des vitesses.

En effectuant un passage à la limite, il apparaît un paradoxe analogue à celui de Selleri : l'addition des vitesses devient galiléenne dans un repère inertiel.

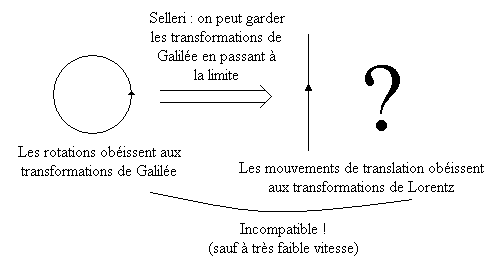
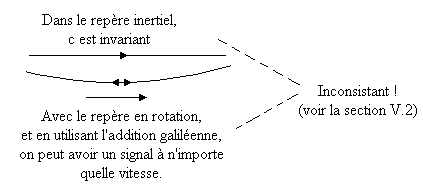
Avec des arcs de cercles qui sont quasiment des segments de droite, et en utilisant un signal allant dans le sens approprié, il y a même la possibilité d'avoir des signaux allant plus vite que c entre deux points quelconques. Or, cela viole la causalité et conduit donc à des inconsistances en relativité restreinte.

L'addition galiléenne des vitesses est compatible avec un espace-temps euclidien mais pas avec un espace-temps de Minkowski qui conduit aux transformations de Lorentz. Ces relations sont incompatibles avec les effets relativistes qui sont pourtant observés !

Cette explication montre que la formule donnant la vitesse de la lumière dans un repère tournant est incompatible avec l'invariance de c dans un repère inertiel. Pourtant, nous sommes censés avoir déduit ces relations de la relativité en se basant sur l'invariance de c. Cela semble (en apparence) mener à une inconsistance non seulement de la relativité restreinte, mais des données expérimentales elles-mêmes.

Résultats expérimentaux récents

Au lieu de mesurer la vitesse apparente des signaux, on peut tenter de mesurer la vitesse de la lumière localement, directement. Comme on le fait sans rotation.

Des expériences ont en effet été menées afin de déterminer s'il y avait une anisotropie dans un repère en rotation. En voici quelques-unes effectuées de différentes manières (sources et récepteurs en rotation ou immobiles, mesures sur un aller simple ou un aller-retour).

• Cialdea utilise deux laser multi-modes montés sur une table en rotation et regarde les variations de leur figure d'interférence lorsque la table est mise en rotation. Il obtient une limite supérieure à l'anisotropie de 0,9 m/s.
• Krisher utilise deux masers à hydrogène fixés au sol et séparés par un lien en fibre optique de 21 kilomètres et regarde les variations entre leur phase. Il obtient une limite supérieure à l'anisotropie de 100 m/s.
• Champeney utilise un amortisseur de Moessbauer en rotation et un détecteur fixe pour donner une limite supérieure à l'anisotropie de 3 m/s.
• Turner utilise une source en rotation et un détecteur de Moessbauer fixe pour donner une limite supérieure à l'anisotropie de 10 m/s.
• Gagnon, Torr, Kolen, et Chang ont effectué un test de l'anisotropie avec un guide d'onde. Leurs résultats négatifs sont cohérents avec la relativité restreinte.